
| A. | (-4,0) | B. | [-4,0) | C. | (-∞,-4) | D. | (0,+∞) |
分析 根据题意求出函数的导数并且通过导数求出出原函数的单调区间,进而得到原函数的极值,因为函数存在三个不同的零点,所以结合函数的性质可得函数的极大值大于0,极小值小于0,即可单调答案.
解答 解:由题意可得:f′(x)=3x2-6x.
令f′(x)>0,则x>2或x<0,令f′(x)<0,则0<x<2,
所以函数f(x)的单调增区间为(-∞,0)和(2,+∞),减区间为(0,2),
所以当x=0时函数有极大值f(0)=-k,当x=2时函数有极小值f(2)=-4-k.
因为函数f(x)存在三个不同的零点,
所以f(0)>0并且f(2)<0,
解得:-4<k<0.
所以实数a的取值范围是 (-4,0).
故选:A.
点评 解决此类问题的关键是熟练掌握利用导数求函数的单调区间与函数的极值,并且掌握通过函数零点个数进而判断极值点与0的大小关系


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
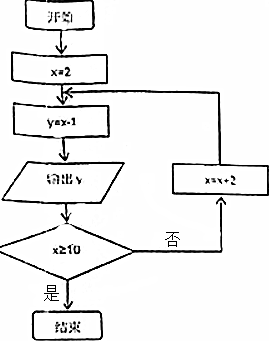 在如图所示的程序框图中,记所有的x的值组成的集合为A,由输出的数据y组成的集合为B.
在如图所示的程序框图中,记所有的x的值组成的集合为A,由输出的数据y组成的集合为B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
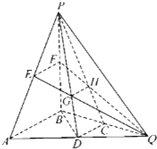 如图,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.
如图,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=b b=a | B. | c=b b=a a=c | C. | b=a a=b | D. | a=c c=b b=a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -2 | C. | 2 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com