
分析 (1)先求出A={x|3<x<6},B={x|x≤4},由此能求出A∪B.
(2)先求出$C=[\frac{15}{8},+∞)$,从而$B∩C=[\frac{15}{8},4]$,再由A∩(B∩C)≠∅,能求出m的取值范围.
解答 解:(1)若log3m=1,∴m=3.…(1分)
∴A={x|3<x<6},又B={x|x≤4},
∴A∪B={x|x<6}.…(4分)
(2)令$\sqrt{x-1}=t(t≥0)$,∴x=t2+1.…(5分)
∴$y=2x-\sqrt{x-1}=2({t^2}+1)-t=2{(t-\frac{1}{4})^2}+\frac{15}{8}$,…(7分)
当$t=\frac{1}{4}$,即$x=\frac{17}{16}$时,$y=2x-\sqrt{x-1}$取得最小值,且最小值为$\frac{15}{8}$.…(8分)
故$C=[\frac{15}{8},+∞)$,从而$B∩C=[\frac{15}{8},4]$,…(9分)
∵A∩(B∩C)≠∅,
∴$\left\{\begin{array}{l}m<4\\ 2m>\frac{15}{8}\\ m<2m\end{array}\right.⇒m∈(\frac{15}{16},4)$.
∴m的取值范围是($\frac{15}{16}$,4].…(12分)
点评 本题考查并集的求法,考查实数的取值范围的求法,是基础题,解题时要认真审题,注意并集、交集的性质的合理运用.


科目:高中数学 来源: 题型:解答题
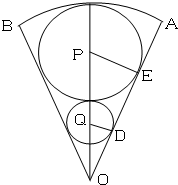 如图,在半径为2,圆心角为变量的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两半径相切并与圆P外切的小圆Q,设圆P与圆Q的半径之积为y.
如图,在半径为2,圆心角为变量的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两半径相切并与圆P外切的小圆Q,设圆P与圆Q的半径之积为y.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最大值$\sqrt{5}$+1和最小值4 | B. | 有最大值5和最小值4 | ||
| C. | 有最大值5和最小值$\sqrt{5}$-1 | D. | 无最大值,最小值4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,0) | B. | [-4,0) | C. | (-∞,-4) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{3\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(0)<f(5) | B. | f(-1)<f(3) | C. | f(3)>f(2) | D. | f(2)>f(0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (1,+∞) | C. | (0,1) | D. | (1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com