
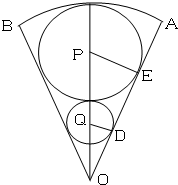
 如图,在半径为2,圆心角为变量的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两半径相切并与圆P外切的小圆Q,设圆P与圆Q的半径之积为y.
如图,在半径为2,圆心角为变量的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两半径相切并与圆P外切的小圆Q,设圆P与圆Q的半径之积为y.分析 (1)①设圆P与圆Q的半径分别为R、r.由R=(2-R)•sinθ得$R=\frac{2sinθ}{1+sinθ}$,由此能将y表示成θ的函数.
②圆Q的半径为r,由$\frac{r}{x}=\frac{2-2x-r}{2-x}$,能将y表示成x的函数.
(2)选择②:由y=-x3+x2(0<x<1)得y'=-3x2+2x(0<x<1),由此利用导数性质能求出y的最大值.
解答 解:(1)①如图,设圆P与圆Q的半径分别为R、r.
由R=(2-R)•sinθ得$R=\frac{2sinθ}{1+sinθ}$,
又$\frac{r}{R}=\frac{2-2R-r}{2-R}$,
∴$r=R-{R^2}=\frac{2sinθ}{1+sinθ}-{(\frac{2sinθ}{1+sinθ})^2}=\frac{2sinθ•(1-sinθ)}{{{{(1+sinθ)}^2}}}$,
∴$y=r•R=\frac{{4{{sin}^2}θ({1-sinθ})}}{{{{({1+sinθ})}^3}}}(0<θ<\frac{π}{2})$.(5分)
②圆Q的半径为r,由$\frac{r}{x}=\frac{2-2x-r}{2-x}$得r=x-x2,
∴y=r•x=-x3+x2(0<x<1).(10分)
(2)选择②:由y=-x3+x2(0<x<1)得y'=-3x2+2x(0<x<1),
令y'>0,得$0<x<\frac{2}{3}$; 令y'<0,得$\frac{2}{3}<x<1$.
∴y=-x3+x2(0<x<1)在区间$(0,\frac{2}{3})$上是增函数,在区间$(\frac{2}{3},1)$上是减函数.
∴当$x=\frac{2}{3}$时,${y_{max}}=\frac{4}{27}$.(15分)
点评 本题考查函数解析式的求法,考查函数值的最大值的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -2 | C. | 2 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com