
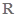 上的单调函数
上的单调函数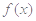 满足
满足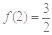 ,且对任意
,且对任意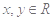 都有
都有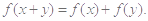
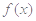 为奇函数;
为奇函数;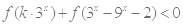 对任意
对任意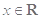 恒成立,求实数
恒成立,求实数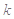 的取值范围.
的取值范围.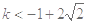 .
.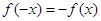 或
或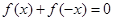 ,由此在已知式
,由此在已知式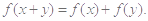 里设
里设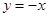 ,从而有
,从而有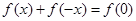 ,因此我们还要先求出
,因此我们还要先求出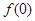 ,这个只要设
,这个只要设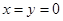 或者有一个为0即可得
或者有一个为0即可得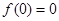 ,故可证得
,故可证得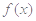 为奇函数;(2)不等式
为奇函数;(2)不等式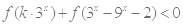 可以利用
可以利用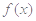 为奇函数的结论,变形为
为奇函数的结论,变形为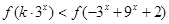 ,再利用函数的单调性去掉符号“
,再利用函数的单调性去掉符号“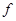 ”,转化为关于
”,转化为关于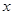 的不等式恒成立问题,即
的不等式恒成立问题,即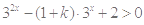 对任意
对任意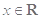 成立,这时还需要用换元法(设
成立,这时还需要用换元法(设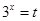 )变化二次不等式怛成立,当然不要忘记
)变化二次不等式怛成立,当然不要忘记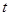 的取值范围.
的取值范围.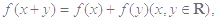 ①
①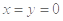 ,代入①式,得
,代入①式,得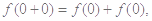 即
即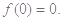
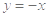 ,代入①式,得
,代入①式,得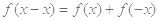 ,又
,又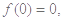
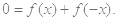 即
即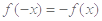 对任意
对任意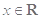 成立,
成立,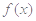 是奇函数. 4分
是奇函数. 4分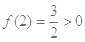 ,即
,即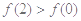 ,又
,又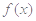 在
在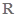 上是单调函数,
上是单调函数,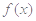 在
在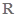 上是增函数.
上是增函数.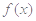 是奇函数.
是奇函数.
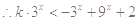 ,即
,即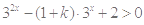 对任意
对任意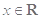 成立.
成立.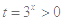 ,问题等价于
,问题等价于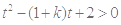 对任意
对任意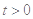 恒成立. 8分
恒成立. 8分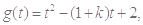 其对称轴
其对称轴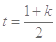 .
.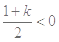 时,即
时,即 时,
时,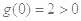 ,符合题意; 10分
,符合题意; 10分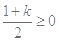 时,对任意
时,对任意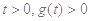 恒成立
恒成立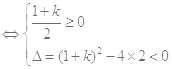
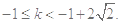 12分
12分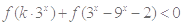 对任意
对任意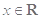 恒成立时,
恒成立时,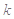 的取值范围是:
的取值范围是: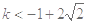 . 13分
. 13分

科目:高中数学 来源:不详 题型:解答题
 毫克)与时间
毫克)与时间 (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后, 与
与 的函数关系式为
的函数关系式为 (
( 为常数),如图所示,根据图中提供的信息,回答下列问题:
为常数),如图所示,根据图中提供的信息,回答下列问题:
 (毫克)与时间
(毫克)与时间 (小时)之间的函数关系式;
(小时)之间的函数关系式;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
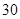 天内每件的销售价格
天内每件的销售价格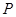 (元)与时间
(元)与时间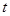 (天)的函数关系是
(天)的函数关系是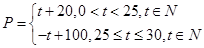 该商品的日销售量
该商品的日销售量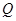 (件)与时间
(件)与时间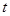 (天)的函数关系是
(天)的函数关系是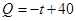
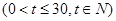 ,设商品的日销售额为
,设商品的日销售额为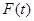 (销售量与价格之积)
(销售量与价格之积)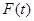 的解析式;
的解析式;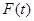 的最大值.
的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com