
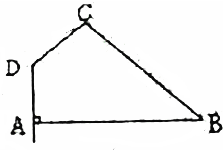
分析 几何体为圆台挖去一个圆锥,求出圆台和圆锥的底面半径,高和母线,代入面积公式和体积公式计算即可.
解答 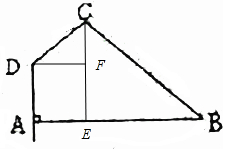 解:作CE⊥AB于E,作DF⊥CE于F,
解:作CE⊥AB于E,作DF⊥CE于F,
则AE=AD=2,CE=4,BE=3,∴BC=5,
四边形ABCD绕AD旋转一周所成几何体为圆台挖去一个圆锥,
其中,圆台的上下底面半径为r1=2,r2=5,高为4,母线l=5,
圆锥的底面半径为2,高为2,母线l′=2$\sqrt{2}$,
∴几何体的表面积S=25π+π×2×5+π×5×5+$π×2×2\sqrt{2}$=60π+4$\sqrt{2}$π.
几何体的体积V=$\frac{1}{3}$(25π+4π+$\sqrt{25π•4π}$)×4-$\frac{1}{3}$×4π×2=$\frac{148π}{3}$.
点评 本题考查了旋转体的结构特征,面积和体积计算,属于中档题.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平行于同一直线的两直线平行 | |
| B. | 垂直于同一直线的两直线平行 | |
| C. | 平行于同一平面的两平面不一定平行 | |
| D. | 垂直于同一平面的两平面平行 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com