解答:
解:(Ⅰ)函数f(x)的定义域为(-1,+∞),f′(x)=
,
①当1<a<2时,若x∈(-1,a
2-2a),则f′(x)>0,此时函数f(x)在(-1,a
2-2a)上是增函数,
若x∈(a
2-2a,0),则f′(x)<0,此时函数f(x)在(a
2-2a,0)上是减函数,
若x∈(0,+∞),则f′(x)>0,此时函数f(x)在(0,+∞)上是增函数.
②当a=2时,f′(x)>0,此时函数f(x)在(-1,+∞)上是增函数,
③当a>2时,若x∈(-1,0),则f′(x)>0,此时函数f(x)在(-1,0)上是增函数,
若x∈(0,a
2-2a),则f′(x)<0,此时函数f(x)在(0,a
2-2a)上是减函数,
若x∈(a
2-2a,+∞),则f′(x)>0,此时函数f(x)在(a
2-2a,+∞)上是增函数.
(Ⅱ)由(Ⅰ)知,当a=2时,此时函数f(x)在(-1,+∞)上是增函数,
当x∈(0,+∞)时,f(x)>f(0)=0,
即ln(x+1)>
,(x>0),
又由(Ⅰ)知,当a=3时,f(x)在(0,3)上是减函数,
当x∈(0,3)时,f(x)<f(0)=0,ln(x+1)<
,
下面用数学归纳法进行证明
<a
n≤
成立,
①当n=1时,由已知
<a1=1,故结论成立.
②假设当n=k时结论成立,即
<ak≤,
则当n=k+1时,a
n+1=ln(a
n+1)>ln(
+1)
>=,
a
n+1=ln(a
n+1)<ln(
+1)
<=,
即当n=k+1时,
<ak+1≤成立,
综上由①②可知,对任何n∈N
•结论都成立.



 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案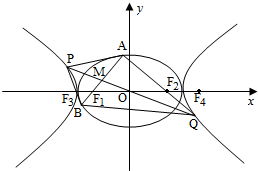 如图,O为坐标原点,椭圆C1:
如图,O为坐标原点,椭圆C1: