
【题目】设函数f(x)=2x+1的定义域为[1,5],则函数f(2x﹣3)的定义域为( )
A.[1,5]
B.[3,11]
C.[3,7]
D.[2,4]
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ,且
,且![]() 为常数).
为常数).
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若对于任意的![]() ,都有
,都有![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(3)若方程![]() 在
在![]() 上有且只有一个实根,求
上有且只有一个实根,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区以“绿色出行”为宗旨开展“共享单车”业务.该地有![]() ,
, ![]() 两种“共享单车”(以下简称
两种“共享单车”(以下简称![]() 型车,
型车, ![]() 型车).某学习小组7名同学调查了该地区共享单车的使用情况.
型车).某学习小组7名同学调查了该地区共享单车的使用情况.
(Ⅰ)某日该学习小组进行一次市场体验,其中4人租到![]() 型车,3人租到
型车,3人租到![]() 型车.如果从组内随机抽取2人,求抽取的2人中至少有一人在市场体验过程中租到
型车.如果从组内随机抽取2人,求抽取的2人中至少有一人在市场体验过程中租到![]() 型车的概率;
型车的概率;
(Ⅱ)根据已公布的2016年该地区全年市场调查报告,小组同学发现3月,4月的用户租车情况城现如表使用规律.例如,第3个月租![]() 型车的用户中,在第4个月有
型车的用户中,在第4个月有![]() 的用户仍租
的用户仍租![]() 型车.
型车.
第3个月 第4个月 | 租用 | 租用 |
租用 |
|
|
租用 |
|
|
若认为2017年该地区租用单车情况与2016年大致相同.已知2017年3月该地区租用![]() ,
,![]() 两种车型的用户比例为1:1,根据表格提供的信息,估计2017年4月该地区租用两种车型的用户比例.
两种车型的用户比例为1:1,根据表格提供的信息,估计2017年4月该地区租用两种车型的用户比例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:在等式![]()
![]()
![]()
![]() 中,把
中,把![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() 叫做三项式的
叫做三项式的![]() 次系数列(如三项式的1次系数列是1,1,1).
次系数列(如三项式的1次系数列是1,1,1).
(1)填空:三项式的2次系数列是_______________;
三项式的3次系数列是_______________;
(2)由杨辉三角数阵表可以得到二项式系数的性质![]() ,类似的请用三项式
,类似的请用三项式![]() 次系数列中的系数表示
次系数列中的系数表示![]() (无须证明);
(无须证明);
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列几种说法: ①若logablog3a=1,则b=3;
②若a+a﹣1=3,则a﹣a﹣1= ![]() ;
;
③f(x)=log(x+ ![]() 为奇函数;
为奇函数;
④f(x)= ![]() 为定义域内的减函数;
为定义域内的减函数;
⑤若函数y=f(x)是函数y=ax(a>0且a≠1)的反函数,且f(2)=1,则f(x)=log ![]() x,其中说法正确的序号为 .
x,其中说法正确的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系,将曲线![]() 上的每一个点的横坐标保持不变,纵坐标缩短为原来的
上的每一个点的横坐标保持不变,纵坐标缩短为原来的![]() ,得到曲线
,得到曲线![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,
轴的正半轴为极轴,建立极坐标系, ![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的参数方程;
的参数方程;
(Ⅱ)过原点![]() 且关于
且关于![]() 轴对称的两条直线
轴对称的两条直线![]() 与
与![]() 分别交曲线
分别交曲线![]() 于
于![]() 、
、![]() 和
和![]() 、
、![]() ,且点
,且点![]() 在第一象限,当四边形
在第一象限,当四边形![]() 的周长最大时,求直线
的周长最大时,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的右焦点为F,右顶点为A,设离心率为e,且满足
的右焦点为F,右顶点为A,设离心率为e,且满足![]() ,其中O为坐标原点.
,其中O为坐标原点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点![]() 的直线l与椭圆交于M,N两点,求△OMN面积的最大值.
的直线l与椭圆交于M,N两点,求△OMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图象如图所示.
的部分图象如图所示.
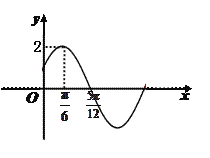
(1) 求函数![]() 的解析式;
的解析式;
(2) 如何由函数![]() 的通过适当图象的变换得到函数
的通过适当图象的变换得到函数![]() 的图象, 写出变换过程;
的图象, 写出变换过程;
(3) 若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com