Question

18．给出下列命题：
（1）一组对边和一组对角分别相等的四边形是平行四边形；
（2）两组对角的内角平分线分别平行的四边形是平行四边形；
（3）一组对边中点间的距离等于另一组对边长和的一半的四边形是平行四边形；
（4）两条对角线都平分四边形面积的四边形是平行四边形．
 其中真命题是（2），（4）．（写出所有真命题的编号）

Answer 1

分析 对四个命题分别进行判断，即可得出结论．

解答 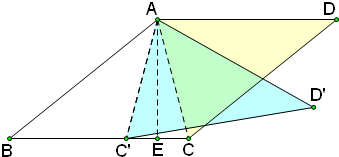解：（1）一组对边和一组对角分别相等的四边形不一定是平行四边形，如图，四边形ABCD为平行四边形，连接AC，作AE垂直BC于E；
在EB上截取EC'=EC，连接AC'，则△AEC'≌△AEC，AC'=AC．
把△ACD绕点A顺时针旋转∠CAC'的度数，则AC与AC'重合．
显然四边形ABC'D'满足：AB=CD=C'D'；∠B=∠D=∠D'，而四边形ABC'D'并不是平行四边形．不正确；
（2）两组对角的内角平分线分别平行的四边形，则两组对角相等，故四边形一定是平行四边形，正确；
（3）一组对边中点间的距离等于另一组对边长和的一半的四边形是平行四边形，也可以是梯形，不正确；
（4）两条对角线都平分四边形面积的四边形，由三角形全等，可得是平行四边形，正确．
故答案为：（2），（4）．

点评 本题考查命题的真假判断，考查平行四边形的判断，考查学生分析解决问题的能力，属于中档题．