
【题目】在平面内将点A(2,1)绕原点按逆时针方向旋转 ![]() ,得到点B,则点B的坐标为 .
,得到点B,则点B的坐标为 .
【答案】(﹣ ![]() ,
, ![]() )
)
【解析】解:如图,作AC⊥x轴于C点,BD⊥x轴于D点, 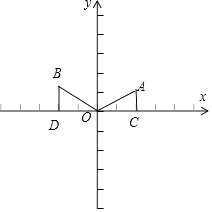
∵点A的坐标为(2,1),
∴AC=1,OC=2,
∴OA= ![]() =
= ![]() ,
,
∴sin∠AOC= ![]() ,cos∠AOC=
,cos∠AOC= ![]() ,
,
∵OA绕原点按逆时针方向旋转 ![]() 得OB,
得OB,
∴∠AOB= ![]() ,OA=OB=
,OA=OB= ![]() ,
,
∴∠BOC=∠AOC+ ![]() ,
,
∴sin∠BOC=sin(∠AOC+ ![]() )=sin∠AOCcos
)=sin∠AOCcos ![]() +cos∠AOCsin
+cos∠AOCsin ![]() =
= ![]() ×(﹣
×(﹣ ![]() )+
)+ ![]() ×
× ![]() =
= ![]() ,
,
cos∠BOC=cos(∠AOC+ ![]() )=cos∠AOCcos
)=cos∠AOCcos ![]() ﹣sin∠AOCsin
﹣sin∠AOCsin ![]() =
= ![]() ×(﹣
×(﹣ ![]() )﹣
)﹣ ![]() ×
× ![]() =﹣
=﹣ ![]() ,
,
∴DB=OBsin∠BOC= ![]() ×
× ![]() =
= ![]() ,OD=OBcos∠BOC=
,OD=OBcos∠BOC= ![]() ×(﹣
×(﹣ ![]() )=﹣
)=﹣ ![]() ,
,
∴B点坐标为:(﹣ ![]() ,
, ![]() ).
).
故答案为:(﹣ ![]() ,
, ![]() ).
).
AC⊥x轴于C点,BD⊥x轴于D点,由点A的坐标得到AC,OC,可求sin∠AOC,cos∠AOC,再根据旋转的性质得到∠BOC=∠AOC+ ![]() ,OA=OB,利用两角和的正弦函数,余弦函数公式即可得到B点坐标.
,OA=OB,利用两角和的正弦函数,余弦函数公式即可得到B点坐标.


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
【题目】如图,椭圆C: ![]() +
+ ![]() =1(a>b>0)的左焦点为F1(﹣1,0),离心率是e,点(1,e)在椭圆上.
=1(a>b>0)的左焦点为F1(﹣1,0),离心率是e,点(1,e)在椭圆上. 
(1)求椭圆C的方程;
(2)设点M(2,0),过点F1的直线交C于A,B两点,直线MA,MB与直线x=﹣2分别交于P,Q两点,求△MPQ面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在六面体ABCD﹣A1B1C1D1中,M,N分别是棱A1B1 , B1C1的中点,平面ABCD⊥平面A1B1BA,平面ABCD平面B1BCC1 . 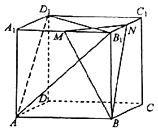
(1)证明:BB1⊥平面ABCD;
(2)已知六面体ABCD﹣A1B1C1D1的棱长均为 ![]() ,cos∠BAD=
,cos∠BAD= ![]() ,设平面BMN与平面AB1D1相交所成二面角的大小为θ求cosθ.
,设平面BMN与平面AB1D1相交所成二面角的大小为θ求cosθ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李冶(1192﹣1279),真定栾城(今属河北石家庄市)人,金元时期的数学家、诗人、晚年在封龙山隐居讲学,数学著作多部,其中《益古演段》主要研究平面图形问题:求圆的直径,正方形的边长等,其中一问:现有正方形方田一块,内部有一个圆形水池,其中水池的边缘与方田四边之间的面积为13.75亩,若方田的四边到水池的最近距离均为二十步,则圆池直径和方田的边长分别是(注:240平方步为1亩,圆周率按3近似计算)( )
A.10步、50步
B.20步、60步
C.30步、70步
D.40步、80步
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设M、N、T是椭圆 ![]() 上三个点,M、N在直线x=8上的摄影分别为M1、N1 .
上三个点,M、N在直线x=8上的摄影分别为M1、N1 .
(Ⅰ)若直线MN过原点O,直线MT、NT斜率分别为k1 , k2 , 求证k1k2为定值.
(Ⅱ)若M、N不是椭圆长轴的端点,点L坐标为(3,0),△M1N1L与△MNL面积之比为5,求MN中点K的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在五棱锥P﹣ABCDE中,△ABE是等边三角形,四边形BCDE是直角梯形且∠DEB=∠CBE=90°,G是CD的中点,点P在底面的射影落在线段AG上.
(Ⅰ)求证:平面PBE⊥平面APG;
(Ⅱ)已知AB=2,BC= ![]() ,侧棱PA与底面ABCDE所成角为45°,S△PBE=
,侧棱PA与底面ABCDE所成角为45°,S△PBE= ![]() ,点M在侧棱PC上,CM=2MP,求二面角M﹣AB﹣D的余弦值.
,点M在侧棱PC上,CM=2MP,求二面角M﹣AB﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l与平面α相交但不垂直,m为空间内一条直线,则下列结论一定不成立的是( )
A.m⊥l,mα
B.m⊥l,m∥α
C.m∥l,m∩α≠
D.m⊥l,m⊥α
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com