
【题目】已知函数![]() 为偶函数,且函数
为偶函数,且函数
![]() 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为![]() .
.
(1)求![]() 的值;
的值;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后,再将得到的图象上各点的横坐标伸长到原来的
个单位后,再将得到的图象上各点的横坐标伸长到原来的![]() 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数![]() 的图象,求
的图象,求![]() 的单调递减区间.
的单调递减区间.
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,某公司要在A、B两地连线上的定点C处建造广告牌CD,其中D为顶端,AC长35米,CB长80米,设点A、B在同一水平面上,从A和B看D的仰角分别为α和β. 
(1)设计中CD是铅垂方向,若要求α≥2β,问CD的长至多为多少(结果精确到0.01米)?
(2)施工完成后,CD与铅垂方向有偏差,现在实测得α=38.12°,β=18.45°,求CD的长(结果精确到0.01米).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个机器人每一秒钟前进一步或后退一步,程序设计师设计的程序是让机器人以先前进3步,然后再后退2步的规律移动.如果将机器人放在数轴的原点,面向正的方向在数轴上移动(1步的距离为1个单位长度).令![]() 表示第
表示第![]() 秒时机器人所在位置的坐标,且记
秒时机器人所在位置的坐标,且记![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系中,点A,B,C的坐标分别为A(cosα,sinα),B(2,0),C(0,2),α∈(0,π).
(1)若![]() ,求α的值;
,求α的值;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出了2010年亚洲某些国家的国民平均寿命![]() 单位:岁
单位:岁![]() .
.
国家 | 平均寿命 | 国家 | 平均寿命 | 国家 | 平均寿命 |
阿曼 |
| 阿富汗 | 59 | 巴基斯坦 |
|
巴林 | | 阿联酋 |
| 马来西亚 |
|
朝鲜 |
| 东帝汶 |
| 孟加拉国 |
|
韩国 |
| 柬埔寨 |
| 塞浦路斯 |
|
老挝 |
| 卡塔尔 |
| 沙特阿拉伯 |
|
蒙古 |
| 科威特 | | 哈萨克斯坦 |
|
缅甸 |
| 菲律宾 |
| 印度尼西亚 |
|
日本 |
| 黎巴嫩 |
| 土库曼斯坦 | 65 |
泰国 |
| 尼泊尔 | 68 | 吉尔吉斯斯坦 |
|
约旦 |
| 土耳其 |
| 乌兹别克斯坦 |
|
越南 | 75 | 伊拉克 |
| 也门 |
|
中国 |
| 以色列 |
| 文莱 |
|
伊朗 | 74 | 新加坡 |
| 叙利亚 |
|
印度 |
|
![]() 根据这40个国家的样本数据,得到如图所示的频率分布直方图,其中样本数据的分组区间为:
根据这40个国家的样本数据,得到如图所示的频率分布直方图,其中样本数据的分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 请根据上述所提供的数据,求出频率分布直方图中的a,b;
请根据上述所提供的数据,求出频率分布直方图中的a,b;
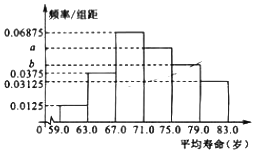
![]() 请根据统计思想,利用
请根据统计思想,利用![]() 中的频率分布直方图估计亚洲人民的平均寿命及国民寿命的中位数
中的频率分布直方图估计亚洲人民的平均寿命及国民寿命的中位数![]() 保留一位小数
保留一位小数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=Asin(ωx+φ)(A>0,ω>0,![]() )的图象过点
)的图象过点![]() ,图象与P点最近的一个最高点坐标为
,图象与P点最近的一个最高点坐标为![]() .
.
(1)求函数解析式;
(2)求函数的最小值,并写出相应的x值的集合;
(3)当![]() 时,求函数的值域.
时,求函数的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是从上下底面处在水平状态下的棱长为a的正方体ABCD﹣A1B1C1D1中分离出来的: 
(1)试判断A1是否在平面B1CD内;(回答是与否)
(2)求异面直线B1D1与C1D所成的角;
(3)如果用图示中这样一个装置来盛水,那么最多可以盛多少体积的水.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f1(x)=![]() x2,f2(x)=alnx(其中a>0).
x2,f2(x)=alnx(其中a>0).
(1)求函数f(x)=f1(x)·f2(x)的极值;
(2)若函数g(x)=f1(x)-f2(x)+(a-1)x在区间(![]() ,e)内有两个零点,求正实数a的取值范围;
,e)内有两个零点,求正实数a的取值范围;
(3)求证:当x>0时,![]() .(说明:e是自然对数的底数,e=2.71828…)
.(说明:e是自然对数的底数,e=2.71828…)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com