
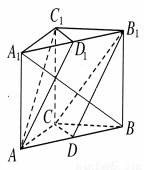
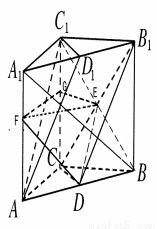
如图所示,在三棱柱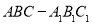 中,
中,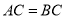 ,
,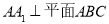 ,点
,点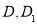 分别是
分别是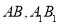 的中点.
的中点.
(1)求证:平面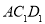 ∥平面
∥平面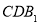 ;
;
(2)求证:平面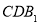 ⊥平面
⊥平面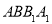 ;
;
(3)若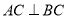 ,
,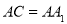 ,求异面直线
,求异面直线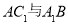 所成的角。
所成的角。
(1) 详见解析(2) 详见解析(3)详见解析
【解析】
试题分析:(1)根据平面几何可证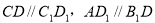 ,可证得面面垂直;(2)根据D是AB的中点,可证
,可证得面面垂直;(2)根据D是AB的中点,可证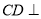 面
面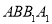 ,证得面面垂直;(3)异面直线所成的角,转化成相交直线所成的角,然后在所在三角形内解决角的问题.
,证得面面垂直;(3)异面直线所成的角,转化成相交直线所成的角,然后在所在三角形内解决角的问题.
试题解析:【解析】
(1)证明:在直三棱柱ABC-A1B1C1中,∵点D,D1分别是AB,A1B1的中点,D1B1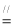 AD∴四边形ADB1D1为平行四边形∴AD1∥DB1∵AD1
AD∴四边形ADB1D1为平行四边形∴AD1∥DB1∵AD1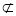 平面CDB1∴AD1//平面CDB1,同理可证C1D1∥平面CDB1∵AD1
平面CDB1∴AD1//平面CDB1,同理可证C1D1∥平面CDB1∵AD1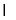 D1C1=D1∴平面AC1D1∥平面CDB 4分
D1C1=D1∴平面AC1D1∥平面CDB 4分
(2)证明:∵AA1⊥平面ABC,CD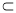 平面ABC∴AA1⊥CD。∵AC=BC
平面ABC∴AA1⊥CD。∵AC=BC
D是AB的中点∴CD⊥AB∵AA1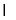 AB=A∴CD⊥平面ABB1A1
AB=A∴CD⊥平面ABB1A1
∵CD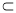 平面ABC∴平面CDB1⊥平面ABB1A1 9分
平面ABC∴平面CDB1⊥平面ABB1A1 9分
(3)连接BC1交B1C于E,连接DE,取AA1中点F,连接EF,又∵D是AB中点,∴AC1 ∥DE,DF∥A1B ∴ ∠EDF是异面直线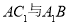 所成的角。设AC=1DE=
所成的角。设AC=1DE=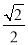 ,DF=
,DF=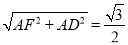 ,EF
,EF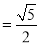 ∴DE2+ DF2= EF2∴∠EDF=90O∴异面直线
∴DE2+ DF2= EF2∴∠EDF=90O∴异面直线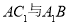 所成的角为90O。13分
所成的角为90O。13分
也可能证明 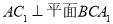 也可得异面直线
也可得异面直线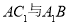 所成的角为90O 13分
所成的角为90O 13分
考点:1.面面垂直的判定;2.面面平行的判定;3.异面直线所成的角.


科目:高中数学 来源:2016届湖南省五市十校高一下学期期中检测数学试卷(解析版) 题型:选择题
设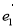 ,
,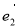 ,
,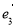 ,
,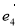 是某平面内的四个单位向量,其中
是某平面内的四个单位向量,其中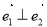 ,
,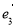 与
与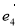 的夹角为45°, 对这个平面内的任意一个向量
的夹角为45°, 对这个平面内的任意一个向量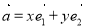 ,规定经过一次“斜二测变换”得到向量
,规定经过一次“斜二测变换”得到向量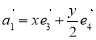 ,设向量
,设向量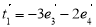 是向量
是向量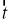 经过一次“斜二测变换”得到的向量,则
经过一次“斜二测变换”得到的向量,则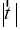 是( )
是( )
A.5 B.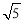 C.73 D.
C.73 D.
查看答案和解析>>
科目:高中数学 来源:2016届湖南张家界市高一下学期第一次月考数学试卷(解析版) 题型:选择题
以A(1,3),B(-5,1)为端点的线段的垂直平分线方程是( )
A. 3x-y+8=0 B. 3x+y+4=0 C . 3x-y+6=0 D. 3x+y+2=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com