
分析 (1)代人m值,利用导函数得出单调性,根据单调性求出最小值;
(Ⅱ)求出导函数,构造函数g(x)=2x2-2mx+1,根据二次函数的性质可知只需g($\frac{3}{2}$)>0,或g($\frac{2}{3}$)>0即可.解不等式求并集即可;
(Ⅲ)利用间接法,求出反面函数f(x)不存在极值点m的范围,再求补集即可.
解答 (Ⅰ) 解:当m=0时,f(x)=lnx+x2,其定义域为(0,+∞),f'(x)=$\frac{1}{x}$+2,
所以f(x)在[1,3]上是增函数,当x=1时,f(x)取得最小值f(1)=1.
故函数f(x)在[1,3]上的最小值为1.
(Ⅱ) 解:依题意,可知f'(x)=$\frac{1}{x}$+2x-2m=$\frac{2{x}^{2}-2mx+1}{x}$,
设g(x)=2x2-2mx+1,则区间[$\frac{2}{3}$,$\frac{3}{2}$]上存在子区间使得不等式g(x)>0成立.
因为函数g(x)的图象是开口向上的抛物线,
所以只要g($\frac{3}{2}$)>0,或g($\frac{2}{3}$)>0即可.
由g($\frac{2}{3}$)>0,即$\frac{2}{9}$-$\frac{4}{3}$m+1>0,解得m<$\frac{11}{12}$,
由g($\frac{3}{2}$)>0,即$\frac{9}{2}$-3m+1>0,解得m<$\frac{11}{6}$,
因此,实数m的取值范围是(-∞,$\frac{11}{6}$).
(Ⅲ) 由(Ⅱ)可知f'(x)=$\frac{1}{x}$+2x-2m,
假设函数f(x)不存在极值点,
∴函数f(x)定义域内恒单调,
∴f'(x)≥0恒成立,
∴$\frac{1}{x}$+2x-2m≥0恒成立,
∴m≤$\sqrt{2}$,
∴若函数存在极值点m的取值范围是($\sqrt{2}$,+∞).
点评 考查了利用导函数判断函数的单调性问题和利用构造法,结合二次函数的图象,利用转化的方法解决实际问题.


科目:高中数学 来源: 题型:解答题
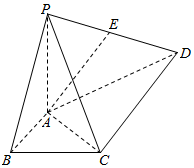 如图,四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=$\frac{π}{2}$,AB=BC=1,CD=2,PA⊥平面ABCD,E是PD的中点.
如图,四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=$\frac{π}{2}$,AB=BC=1,CD=2,PA⊥平面ABCD,E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 编号n | 1 | 2 | 3 | 4 | 5 | 6 |
| 成绩xn | 110 | 124 | 130 | x4 | 110 | 111 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2006 | B. | 4008 | C. | 4012 | D. | 2008 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
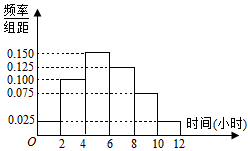 为调查某乡镇中心小学的学生每周平均体育运动时间的情况,收集了20位学生每周平均体育运动时间的样本数据(单位:小时).这20位学生每周平均体育运动时间的频率分布直方图如图所示,其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].
为调查某乡镇中心小学的学生每周平均体育运动时间的情况,收集了20位学生每周平均体育运动时间的样本数据(单位:小时).这20位学生每周平均体育运动时间的频率分布直方图如图所示,其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com