
如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B﹣ACD,点M是棱BC的中点,DM=2 .
.
(1)求证:OM∥平面ABD;
(2)求证:平面DOM⊥平面ABC;
(3)求三棱锥B﹣DOM的体积.

(1)∵O为AC的中点,M为BC的中点,∴OM∥AB.又∵OM?平面ABD,AB?平面ABD,∴OM∥平面ABD.(2)∵在菱形ABCD中,OD⊥AC,∴在三棱锥B-ACD中,OD⊥AC.在菱形ABCD中,AB=AD=4,
∠BAD=60°,可得BD=4.∵O为BD的中点,∴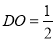 ,BD=2.∵O为AC的中点,M为BC的中点,∴
,BD=2.∵O为AC的中点,M为BC的中点,∴ ,AB=2.因此,
,AB=2.因此, ,可得OD⊥OM.∵AC、OM是平面ABC内的相交直线,∴OD⊥平面ABC.∵OD?平面DOM,∴平面DOM⊥平面ABC.(3)
,可得OD⊥OM.∵AC、OM是平面ABC内的相交直线,∴OD⊥平面ABC.∵OD?平面DOM,∴平面DOM⊥平面ABC.(3) .
.
【解析】
试题分析:(1)利用三角形中位线定理,证出OM∥AB,结合线面平行判定定理,即可证出OM∥平面ABD.
(2)根据题中数据,算出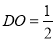 ,BD=2,
,BD=2, ,AB=2,从而得到
,AB=2,从而得到 ,可得OD⊥OM.结合OD⊥AC利用线面垂直的判定定理,证出OD⊥平面ABC,从而证出平面DOM⊥平面ABC.
,可得OD⊥OM.结合OD⊥AC利用线面垂直的判定定理,证出OD⊥平面ABC,从而证出平面DOM⊥平面ABC.
(3)由(2)得到OD为三棱锥D-BOM的高.算出△BOM的面积,利用锥体体积公式算出三棱锥D-BOM的体积,即可得到三棱锥B-DOM的体积.
试题解析:(1)∵O为AC的中点,M为BC的中点,∴OM∥AB.
又∵OM?平面ABD,AB?平面ABD,∴OM∥平面ABD.
(2)∵在菱形ABCD中,OD⊥AC,∴在三棱锥B-ACD中,OD⊥AC.
在菱形ABCD中,AB=AD=4,∠BAD=60°,可得BD=4.
∵O为BD的中点,∴DO= ,BD=2.∵O为AC的中点,M为BC的中点,∴OM=
,BD=2.∵O为AC的中点,M为BC的中点,∴OM= ,AB=2.
,AB=2.
因此, ,可得OD⊥OM.∵AC、OM是平面ABC内的相交直线,∴OD⊥平面ABC.
,可得OD⊥OM.∵AC、OM是平面ABC内的相交直线,∴OD⊥平面ABC.
∵OD?平面DOM,∴平面DOM⊥平面ABC.
(3)由(2)得,OD⊥平面BOM,所以OD是三棱锥D-BOM的高.
由OD=2, ,
,
所以 .
.
考点:线面平行问题;面面垂直问题;三棱锥的体积.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届广东省高二下学期中段考文科数学试卷(解析版) 题型:选择题
某市质量监督局计量认证审查流程图如图示:

从上图可得在审查过程中可能不被通过审查的环节有( )
A.1处 B.2处 C.3处 D.4处
查看答案和解析>>
科目:高中数学 来源:2015届广东省清远市高二下学期期末理科数学试卷(解析版) 题型:填空题
为考察高中生的性别与是否喜欢数学课程之间的关系,在我市某普通中学高中生中随机抽取200名学生,得到如下2×2列联表:
| 喜欢数学课 | 不喜欢数学课 | 合计 |
男 | 30 | 60 | 90 |
女 | 20 | 90 | 110 |
合计 | 50 | 150 | 200 |
经计算K2≈6.06,根据独立性检验的基本思想,约有 _________ (填百分数)的把握认为“性别与喜欢数学课之间有关系”.
查看答案和解析>>
科目:高中数学 来源:2015届广东省清远市高二下学期期末文科数学试卷(解析版) 题型:选择题
设△ABC的三边长分别为a、b、c,△ABC的面积为S,内切圆半径为r,则 ,类比这个结论可知:四面体S﹣ABC的四个面的面积分别为S1、S2、S3、S4,内切球半径为r,四面体S﹣ABC的体积为V,则r=( )
,类比这个结论可知:四面体S﹣ABC的四个面的面积分别为S1、S2、S3、S4,内切球半径为r,四面体S﹣ABC的体积为V,则r=( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届广东省高二下学期期末考试理科数学试卷(解析版) 题型:填空题
已知:长方体 ,
, ,
,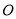 为对角线
为对角线 的中点,过
的中点,过 的直线与长方体表面交于两点
的直线与长方体表面交于两点 ,
, 为长方体表面上的动点,则
为长方体表面上的动点,则 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2015届广东省梅州市高二下学期期中理科数学试卷(解析版) 题型:填空题
从4名男生和3名女生中选出4人担任奥运志愿者,若选出的4人中既有男生又有女生,则不同的选法共有________种.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com