
设△ABC的三边长分别为a、b、c,△ABC的面积为S,内切圆半径为r,则 ,类比这个结论可知:四面体S﹣ABC的四个面的面积分别为S1、S2、S3、S4,内切球半径为r,四面体S﹣ABC的体积为V,则r=( )
,类比这个结论可知:四面体S﹣ABC的四个面的面积分别为S1、S2、S3、S4,内切球半径为r,四面体S﹣ABC的体积为V,则r=( )
A. B.
B.
C. D.
D.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源:2015届广东省高二下学期期末考试理科数学试卷(解析版) 题型:填空题
如图所示,圆 的直径
的直径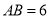 ,
, 为圆周上一点,
为圆周上一点, .过
.过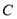 作圆的切线
作圆的切线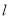 ,过
,过 作
作 的垂线
的垂线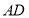 ,
,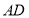 分别与直线
分别与直线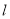 、圆
、圆 交于点
交于点 、
、 ,则线段
,则线段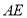 的长为 .
的长为 .

查看答案和解析>>
科目:高中数学 来源:2015届广东省清远市高二下学期期末理科数学试卷(解析版) 题型:解答题
已知向量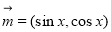 ,
, ,函数
,函数 .
.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)如果△ABC的三边 所对的角分别为
所对的角分别为 、
、 、
、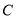 ,且满足
,且满足 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2015届广东省清远市高二下学期期末文科数学试卷(解析版) 题型:解答题
如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B﹣ACD,点M是棱BC的中点,DM=2 .
.
(1)求证:OM∥平面ABD;
(2)求证:平面DOM⊥平面ABC;
(3)求三棱锥B﹣DOM的体积.

查看答案和解析>>
科目:高中数学 来源:2015届广东省清远市高二下学期期末文科数学试卷(解析版) 题型:填空题
如图,AC为⊙O的直径,OB⊥AC,弦BN交AC于点M.若OC= ,OM=1,则MN= _________ .
,OM=1,则MN= _________ .

查看答案和解析>>
科目:高中数学 来源:2015届广东省清远市高二下学期期末文科数学试卷(解析版) 题型:选择题
已知p:x=2,q:0<x<3,则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分,又不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届广东省高二下学期期末考试理科数学试卷(解析版) 题型:解答题
数列{an}中,an>0,an≠1,且 (n∈N*).
(n∈N*).
(1)证明:an≠an+1;
(2)若 ,计算a2,a3,a4的值,并求出数列{an}的通项公式.
,计算a2,a3,a4的值,并求出数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源:2015届广东省梅州市高二下学期期中理科数学试卷(解析版) 题型:选择题
函数y=x2cosx的导数为( )
A.y′=2xcosx-x2sinx B.y′=2xcosx+x2sinx
C.y′=x2cosx-2xsinx D.y′=xcosx-x2sinx
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com