
���� ��1������Բ�ɽ�������F��1��0������$\frac{p}{2}$=1���������������C�Ĺ��̣�
��2����ֱ�߷��̴�����Բ���̣��ɡ���0������Τ�ﶨ����֪x1+x2=$\frac{2{k}^{2}+4}{{k}^{2}}$��x1•x2=1�����������������ʾ$\overrightarrow{MA}$=m$\overrightarrow{AF}$��$\overrightarrow{MB}$=n$\overrightarrow{BF}$���������m=$\frac{{x}_{1}}{1-{x}_{1}}$��n=$\frac{{x}_{2}}{1-{x}_{2}}$�����뼴�����m+n=-1��
��� �⣺��1����Բ��$\frac{x^2}{4}$+$\frac{y^2}{3}$=1�ҽ���F��1��0����
��$\frac{p}{2}$=1��p=2��
��������C�ķ���y2=4x��
��2������֪�ɵã�ֱ��l��б��һ�����ڣ�
����l��y=k��x-1����l��y�ύ��M��0��-k����
��ֱ��l�������߽���A��x1��y1��B��x2��y2����
��$\left\{\begin{array}{l}{y=k��x-1��}\\{{y}^{2}=4x}\end{array}\right.$����k2x2-2��k2+2��+k2=0��
��=4��k2+2��2-4k4=16��k2+1����0��
��x1+x2=$\frac{2{k}^{2}+4}{{k}^{2}}$��x1•x2=1��
$\overrightarrow{MA}$=m$\overrightarrow{AF}$��
�ࣨx1��y1+k��=m��1-x1��-y1����
x1=m��1-x1��
��m=$\frac{{x}_{1}}{1-{x}_{1}}$��ͬ��n=$\frac{{x}_{2}}{1-{x}_{2}}$��
m+n=$\frac{{x}_{1}}{1-{x}_{1}}$+$\frac{{x}_{2}}{1-{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}-2{x}_{1}{x}_{2}}{1-��{x}_{1}+{x}_{2}��+{x}_{1}•{x}_{2}}$=-1��
�ʶ������ֱ��l��m+n��ֵ-1��
���� ���⿼�������ߵı����̼�������ʣ�����ֱ���������ߵ�λ�ù�ϵ��Τ�ﶨ����Ӧ�ã�������������������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
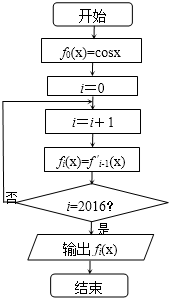
| A�� | sinx | B�� | -sinx | C�� | cosx | D�� | -cosx |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | k��-1 | B�� | k��-1 | C�� | k��2 | D�� | k��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
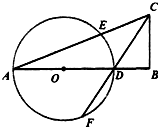 ��ͼ����ֱ֪��������ABC����BΪֱ�ǣ���C��ƽ���߽�AB��D����ADΪֱ����ԲO����AC�ڵ�E����CD��F��
��ͼ����ֱ֪��������ABC����BΪֱ�ǣ���C��ƽ���߽�AB��D����ADΪֱ����ԲO����AC�ڵ�E����CD��F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com