
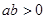 ,且
,且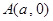 、
、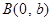 、
、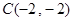 三点共线,则
三点共线,则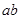 的最小值为 .
的最小值为 .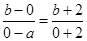 ,化简可得2a+2b+ab=0,即ab=-2a-2b,若ab>0,要么a>0且b>0,要么a<0且b<0,直线经过第三象限的C(-2,-2),由直线的性质可知,a<0,b<0,因为a<0,b<0,所以-2a-2b>0且-2a-2b≥2
,化简可得2a+2b+ab=0,即ab=-2a-2b,若ab>0,要么a>0且b>0,要么a<0且b<0,直线经过第三象限的C(-2,-2),由直线的性质可知,a<0,b<0,因为a<0,b<0,所以-2a-2b>0且-2a-2b≥2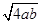 =4
=4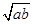 又因为ab=-2a-2b,所以ab≥4
又因为ab=-2a-2b,所以ab≥4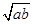 ,即ab-4
,即ab-4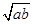 ≥0,令t=
≥0,令t=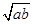 >0,可得t2-4t≥0,解可得t≥4或t≤0,又由t>0,则t≥4,即
>0,可得t2-4t≥0,解可得t≥4或t≤0,又由t>0,则t≥4,即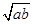 ≥4,ab≥16;则ab的最小值为16;故答案为16.
≥4,ab≥16;则ab的最小值为16;故答案为16.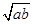 ,进而由一元二次不等式的性质来求解
,进而由一元二次不等式的性质来求解

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com