
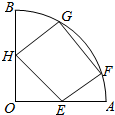
 如图,四边形EFGH是圆心角为60°,半径为R的扇形的内接矩形,点F,G在$\widehat{AB}$上,求四边形EFGH的最大面积.
如图,四边形EFGH是圆心角为60°,半径为R的扇形的内接矩形,点F,G在$\widehat{AB}$上,求四边形EFGH的最大面积. 分析 求最大值问题这里应构造函数,怎么选择便于以此表达矩形面积的自变量
解答 解:设∠FOA=θ,则GF=2Rsin(30°-θ),
在△OFE中,∠OEF=150°,故FE=2Rsinθ
设矩形的面积为S.
那么S=EF•FG=4R2sinθsin(30°-θ)
=2R2[cos(2θ-30°)-cos30°]=2R2[cos(2θ-30°)-$\frac{\sqrt{3}}{2}$]
又∵0<θ<30°,故当cos(2θ-30°)=1即θ=15°时,S取最大值R2(2-$\sqrt{3}$).
点评 本题关键是如何利用角θ表示矩形的长与宽,合理地把长与宽放在三角形中,利用正弦定理或三角定义来表示.


科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1.5 1.65 | B. | 1.6 1.58 | C. | 1.65 1.7 | D. | 1.7 1.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (0,1) | C. | (-∞,1) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\sqrt{3}$ | C. | 3 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 转速x(转/秒) | 8 | 10 | 12 | 14 | 16 |
| 每小时生产有缺点的零件数y(件) | 5 | 7 | 8 | 9 | 11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com