Question

6．一台机器按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器的运转的速度而变化，具有线性相关关系，下表为抽样试验的结果：

转速x（转/秒）	8	10	12	14	16
每小时生产有缺点的零件数y（件）	5	7	8	9	11

（1）如果y对x有线性相关关系，求回归方程；
（2）若实际生产中，允许每小时生产的产品中有缺点的零件最多有10个，那么机器的运转速度应控制在设么范围内？参考公式：$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$，$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$．

Answer 1

分析 （1）先做出横标和纵标的平均数，做出利用最小二乘法求线性回归方程的系数的量，做出系数，求出a，写出线性回归方程．
（2）根据上一问做出的线性回归方程，使得函数值小于或等于10，解出不等式．

解答 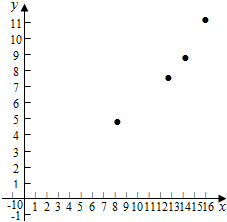解：（1）$\overline{x}$=12，$\overline{y}$=8，
40+70+96+126+176-5×12×8=28，
64+100+144+196+256-5×144=40，
∴b=0.7，a=8-0.7×12=-0.4
∴回归直线方程为：y=0.7x-0.4；
（3）由上一问可知0.7x-0.4≤10，
解得x≤14.85．

点评 本题考查线性回归分析，考查线性回归方程，考查线性回归方程的应用，考查不等式的解法，是一个综合题目．