
”¾ĢāÄæ”æøßĢśŗĶŗ½æյķÉĖŁ·¢Õ¹²»½ö·½±ćĮĖČĖĆĒµÄ³öŠŠ£¬øü“ų¶ÆĮĖĪŅ¹ś¾¼ĆµÄ¾Ž“ó·¢Õ¹£¬¾ŻĶ³¼Ę£¬ŌŚ2018ÄźÕāŅ»ÄźÄŚ“ÓAŹŠµ½BŹŠ³Ė×ųøßĢś»ņ·É»ś³öŠŠµÄ³ÉÄźČĖŌ¼ĪŖ50ĶņČĖ“Ī£®ĪŖĮĖ½ā³ĖæĶ³öŠŠµÄĀśŅā¶Č£¬ĻÖ“ÓÖŠĖ껜³éČ”100ČĖ“Ī×÷ĪŖŃł±¾£®µĆµ½ĻĀ±ķ(µ„Ī»£ŗČĖ“Ī)£ŗ
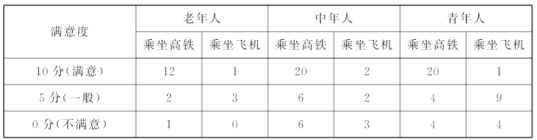
£Ø1£©ŌŚŃł±¾ÖŠČĪČ”1øö£¬ĒóÕāøö³öŠŠČĖĒ”ŗĆ²»ŹĒĒąÄźČĖµÄøÅĀŹ£»
£Ø2£©ŌŚ2018Äź“ÓAŹŠµ½BŹŠ³Ė×ųøßĢśµÄĖłÓŠ³ÉÄźČĖÖŠ£¬Ė껜єȔ2ČĖ“Ī£¬¼ĒĘäÖŠĄĻÄźČĖ³öŠŠµÄČĖ“ĪĪŖX£®ŅŌʵĀŹ×÷ĪŖøÅĀŹ£®ĒóXµÄ·Ö²¼ĮŠŗĶŹżŃ§ĘŚĶū£»
£Ø3£©Čē¹ū¼×½«ŅŖ“ÓAŹŠ³ö·¢µ½BŹŠ£¬ÄĒĆ“øł¾Ż±ķøńÖŠµÄŹż¾Ż£¬Äć½ØŅé¼×ŹĒ³Ė×ųøßĢś»¹ŹĒ ·É»ś£æ²¢ĖµĆ÷ĄķÓÉ.
”¾“š°ø”æ£Ø1£©![]() £Ø2£©¼ū½āĪö£Ø3£©³Ė×ųøßĢś£¬¼ū½āĪö
£Ø2£©¼ū½āĪö£Ø3£©³Ė×ųøßĢś£¬¼ū½āĪö
”¾½āĪö”æ
£Ø1£©øł¾Ż·Ö²ć³éŃłµÄĢŲÕ÷æÉŅŌµĆÖŖ£¬Ńł±¾ÖŠ³öŠŠµÄĄĻÄźČĖ”¢ÖŠÄźČĖ”¢ĒąÄźČĖČĖ“Ī·Ö±šĪŖ19£¬39£¬42£¬¼“æÉ°“ÕչŵäøÅŠĶµÄøÅĀŹ¼ĘĖć¹«Ź½¼ĘĖćµĆ³ö£»
£Ø2£©ŅĄĢāŅāæÉÖŖ![]() ·ž“Ó¶žĻī·Ö²¼£¬ĻČ¼ĘĖć³öĖ껜єȔ1ČĖ“Ī£¬“ĖČĖĪŖĄĻÄźČĖøÅĀŹŹĒ
·ž“Ó¶žĻī·Ö²¼£¬ĻČ¼ĘĖć³öĖ껜єȔ1ČĖ“Ī£¬“ĖČĖĪŖĄĻÄźČĖøÅĀŹŹĒ![]() £¬ĖłŅŌ
£¬ĖłŅŌ![]() £¬¼“
£¬¼“![]() £¬¼“æÉĒó³ö
£¬¼“æÉĒó³ö![]() µÄ·Ö²¼ĮŠŗĶŹżŃ§ĘŚĶū£»
µÄ·Ö²¼ĮŠŗĶŹżŃ§ĘŚĶū£»
£Ø3£©æÉŅŌ¼ĘĖćĀśŅā¶Č¾łÖµĄ“±Č½Ļ³Ė×ųøßĢś»¹ŹĒ·É»ś£®
£Ø1£©ÉčŹĀ¼ž£ŗ”°ŌŚŃł±¾ÖŠČĪČ”1øö£¬Õāøö³öŠŠČĖĒ”ŗĆ²»ŹĒĒąÄźČĖ”±ĪŖ![]() £¬
£¬
ÓɱķæÉµĆ£ŗŃł±¾ÖŠ³öŠŠµÄĄĻÄźČĖ”¢ÖŠÄźČĖ”¢ĒąÄźČĖČĖ“Ī·Ö±šĪŖ19£¬39£¬42£¬
ĖłŅŌŌŚŃł±¾ÖŠČĪČ”1øö£¬Õāøö³öŠŠČĖĒ”ŗĆ²»ŹĒĒąÄźČĖµÄøÅĀŹ![]() £»
£»
£Ø2£©ÓÉĢāŅā£¬![]() µÄĖłÓŠæÉÄÜȔֵĪŖ£ŗ0£¬1£¬2£¬
µÄĖłÓŠæÉÄÜȔֵĪŖ£ŗ0£¬1£¬2£¬
ŅņĪŖŌŚ2018Äź“Ó![]() ŹŠµ½
ŹŠµ½![]() ŹŠ³Ė×ųøßĢśµÄĖłÓŠ³ÉÄźČĖÖŠ£¬Ė껜єȔ1ČĖ“Ī£¬“ĖČĖ
ŹŠ³Ė×ųøßĢśµÄĖłÓŠ³ÉÄźČĖÖŠ£¬Ė껜єȔ1ČĖ“Ī£¬“ĖČĖ
ĪŖĄĻÄźČĖøÅĀŹŹĒ![]() £¬
£¬
ĖłŅŌ![]() £¬
£¬
![]() £¬
£¬
![]() £¬
£¬
ĖłŅŌĖ껜±äĮæ![]() µÄ·Ö²¼ĮŠĪŖ£ŗ
µÄ·Ö²¼ĮŠĪŖ£ŗ
| 0 | 1 | 2 |
|
|
|
|
¹Ź![]() £»
£»
£Ø3£©“ÓĀśŅā¶ČµÄ¾łÖµĄ“·ÖĪöĪŹĢāČēĻĀ£ŗ
ÓɱķæÉÖŖ£¬³Ė×ųøßĢśµÄČĖĀśŅā¶Č¾łÖµĪŖ£ŗ![]() £¬
£¬
³Ė×ų·É»śµÄČĖĀśŅā¶Č¾łÖµĪŖ£ŗ![]() £¬
£¬
ŅņĪŖ![]() £¬
£¬
ĖłŅŌ½ØŅé¼×³Ė×ųøßĢś“Ó![]() ŹŠµ½
ŹŠµ½![]() ŹŠ£®
ŹŠ£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŃ”ŠŽ![]() £ŗ²»µČŹ½Ń”½²
£ŗ²»µČŹ½Ń”½²
ŅŃÖŖŗÆŹżf£Øx£©=|2x+3|+|2x©1|£®
£Ø¢ń£©Ēó²»µČŹ½f£Øx£©£¼8µÄ½ā¼Æ£»
£Ø¢ņ£©Čō¹ŲÓŚxµÄ²»µČŹ½f£Øx£©”Ü|3m+1|ÓŠ½ā£¬Ē󏵏żmµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£¾ŁŠŠŌĖ¶Æ»į£¬ĘäÖŠČż¼¶ĢųŌ¶µÄ³É¼ØŌŚ![]() Ć×ŅŌÉĻµÄ½ųČė¾öČü£¬°ŃĖłµĆµÄ³É¼Ø½ųŠŠÕūĄķŗ󣬷ֳÉ
Ć×ŅŌÉĻµÄ½ųČė¾öČü£¬°ŃĖłµĆµÄ³É¼Ø½ųŠŠÕūĄķŗ󣬷ֳÉ![]() ×黳öʵĀŹ·Ö²¼Ö±·½Ķ¼µÄŅ»²æ·Ö£ØČēĶ¼£©£¬ŅŃÖŖµŚ
×黳öʵĀŹ·Ö²¼Ö±·½Ķ¼µÄŅ»²æ·Ö£ØČēĶ¼£©£¬ŅŃÖŖµŚ![]() ×éµÄʵŹżŹĒ
×éµÄʵŹżŹĒ![]() .
.
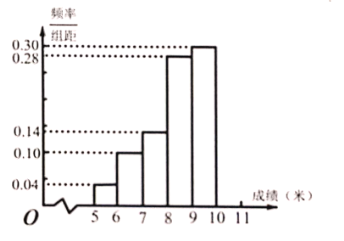
£Ø1£©Ēó½ųČė¾öČüµÄČĖŹż£»
£Ø2£©ÓĆŃł±¾µÄʵĀŹ“śĢęøÅĀŹ£¬¼Ē![]() ±ķŹ¾Į½ČĖÖŠ½ųČė¾öČüµÄČĖŹż£¬Ēó
±ķŹ¾Į½ČĖÖŠ½ųČė¾öČüµÄČĖŹż£¬Ēó![]() µĆ·Ö²¼ĮŠ¼°ŹżŃ§ĘŚĶū.
µĆ·Ö²¼ĮŠ¼°ŹżŃ§ĘŚĶū.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”收ÖÜ÷ĀĖć¾”·ÖŠøų³öĮĖ¹“¹É¶ØĄķµÄ¾ųĆīÖ¤Ć÷.ČēĶ¼ŹĒÕŌĖ¬ĻŅĶ¼¼°×¢ĪÄ.ĻŅĶ¼ŹĒŅ»øöŅŌ¹“¹ÉŠĪÖ®ĻŅĪŖ±ßµÄÕż·½ŠĪ£¬ĘäĆ껿³ĘĪŖĻŅŹµ.Ķ¼ÖŠ°üŗ¬ĖÄøöČ«µČµÄ¹“¹ÉŠĪ¼°Ņ»øöŠ”Õż·½ŠĪ£¬·Ö±šĶæ³ÉÖģÉ«¼°»ĘÉ«£¬ĘäĆ껿³ĘĪŖÖģŹµ”¢»ĘŹµ.ÓÉ2”Į¹“”Į¹É+£Ø¹É£¹“£©2=4”ĮÖģŹµ+»ĘŹµ=ĻŅŹµ£¬»Æ¼ņµĆ¹“2+¹É2=ĻŅ2.ČōĶ¼ÖŠ¹“¹ÉŠĪµÄ¹“¹É±ČĪŖ![]() £¬ĻņĻŅĶ¼ÄŚĖ껜Å×ÖĄ100æÅĶ¼¶¤£Ø“óŠ”ŗöĀŌ²»¼Ę£©£¬ŌņĀäŌŚ»ĘÉ«Ķ¼ŠĪÄŚµÄĶ¼¶¤æÅŹż“óŌ¼ĪŖ£Ø £©£Ø²Īæ¼Źż¾Ż£ŗ
£¬ĻņĻŅĶ¼ÄŚĖ껜Å×ÖĄ100æÅĶ¼¶¤£Ø“óŠ”ŗöĀŌ²»¼Ę£©£¬ŌņĀäŌŚ»ĘÉ«Ķ¼ŠĪÄŚµÄĶ¼¶¤æÅŹż“óŌ¼ĪŖ£Ø £©£Ø²Īæ¼Źż¾Ż£ŗ![]() £¬
£¬![]() £©
£©
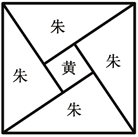
A.2B.4C.6D.8
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ŹĒijµŲijŌĀ1ČÕÖĮ15ČÕµÄČÕĘ½¾łĪĀ¶Č±ä»ÆµÄÕŪĻßĶ¼£¬øł¾ŻøĆÕŪĻßĶ¼£¬ĻĀĮŠ½įĀŪÕżČ·µÄŹĒ£Ø””””£©
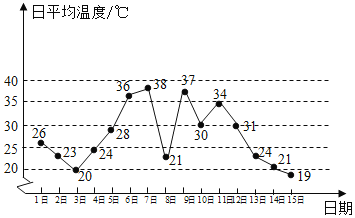
A. Õā15ĢģČÕĘ½¾łĪĀ¶ČµÄ¼«²īĪŖ![]()
B. Į¬ŠųČżĢģČÕĘ½¾łĪĀ¶ČµÄ·½²ī×ī“óµÄŹĒ7ČÕ£¬8ČÕ£¬9ČÕČżĢģ
C. ÓÉÕŪĻßĶ¼ÄÜŌ¤²ā16ČÕĪĀ¶ČŅŖµĶÓŚ![]()
D. ÓÉÕŪĻßĶ¼ÄÜŌ¤²ā±¾ŌĀĪĀ¶ČŠ”ÓŚ![]() µÄĢģŹżÉŁÓŚĪĀ¶Č“óÓŚ
µÄĢģŹżÉŁÓŚĪĀ¶Č“óÓŚ![]() µÄĢģŹż
µÄĢģŹż
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖĢŻŠĪ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬
£¬![]() £¬ĖıߊĪ
£¬ĖıߊĪ![]() ĪŖ¾ŲŠĪ£¬
ĪŖ¾ŲŠĪ£¬![]() £¬Ę½Ćę
£¬Ę½Ćę![]() Ę½Ćę
Ę½Ćę![]() £®
£®

£Ø¢ń£©ĒóÖ¤£ŗ![]() Ę½Ćę
Ę½Ćę![]() £»
£»
£Ø¢ņ£©ĒóĘ½Ćę![]() ÓėĘ½Ćę
ÓėĘ½Ćę![]() Ėł³ÉČń¶žĆę½ĒµÄÓąĻŅÖµ£»
Ėł³ÉČń¶žĆę½ĒµÄÓąĻŅÖµ£»
£Ø¢ó£©ŌŚĻ߶Ī![]() ÉĻŹĒ·ń“ęŌŚµć
ÉĻŹĒ·ń“ęŌŚµć![]() £¬Ź¹µĆÖ±Ļß
£¬Ź¹µĆÖ±Ļß![]() ÓėĘ½Ćę
ÓėĘ½Ćę![]() Ėł³É½ĒµÄÕżĻŅÖµĪŖ
Ėł³É½ĒµÄÕżĻŅÖµĪŖ![]() £¬Čō“ęŌŚ£¬Ēó³öĻ߶Ī
£¬Čō“ęŌŚ£¬Ēó³öĻ߶Ī![]() µÄ³¤£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
µÄ³¤£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅĄÕÕij·¢Õ¹ÖŠ¹ś¼Ņ2018ÄźµÄ¹Ł·½×ŹĮĻ£¬½«øĆ¹śĖłÓŠ¼ŅĶ„°“ÄźŹÕČė“ÓµĶµ½øßµÄĖ³ŠņĘ½¾ł·ÖĪŖĪå×飬ŅĄ“ĪĪŖµŚŅ»×éÖĮµŚĪå×飬ø÷×é¼ŅĶ„µÄÄźŹÕČė×ÜŗĶÕ¼øĆ¹śČ«²æ¼ŅĶ„µÄÄźŹÕČė×ÜŗĶµÄ°Ł·Ö±ČČēĶ¼ĖłŹ¾.
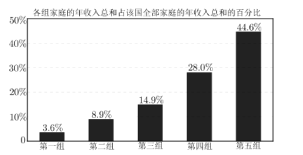
ŅŌĻĀ¹ŲÓŚøĆ¹ś2018Äź¼ŅĶ„ŹÕČėµÄÅŠ¶Ļ£¬Ņ»¶ØÕżČ·µÄŹĒ£Ø £©
A. ÖĮÉŁÓŠ![]() µÄ¼ŅĶ„µÄÄźŹÕČė¶¼µĶÓŚČ«²æ¼ŅĶ„µÄĘ½¾łÄźŹÕČė
µÄ¼ŅĶ„µÄÄźŹÕČė¶¼µĶÓŚČ«²æ¼ŅĶ„µÄĘ½¾łÄźŹÕČė
B. ŹÕČė×īµĶµÄÄĒ![]() µÄ¼ŅĶ„Ę½¾łÄźŹÕČėĪŖČ«²æ¼ŅĶ„Ę½¾łÄźŹÕČėµÄ
µÄ¼ŅĶ„Ę½¾łÄźŹÕČėĪŖČ«²æ¼ŅĶ„Ę½¾łÄźŹÕČėµÄ![]()
C. ŹÕČė×īøßµÄÄĒ![]() µÄ¼ŅĶ„ÄźŹÕČė×ÜŗĶ³¬¹żČ«²æ¼ŅĶ„ÄźŹÕČė×ÜŗĶµÄ
µÄ¼ŅĶ„ÄźŹÕČė×ÜŗĶ³¬¹żČ«²æ¼ŅĶ„ÄźŹÕČė×ÜŗĶµÄ![]()
D. ŹÕČė×īµĶµÄÄĒ![]() µÄ¼ŅĶ„ÄźŹÕČė×ÜŗĶ³¬¹żČ«²æ¼ŅĶ„ÄźŹÕČė×ÜŗĶµÄ
µÄ¼ŅĶ„ÄźŹÕČė×ÜŗĶ³¬¹żČ«²æ¼ŅĶ„ÄźŹÕČė×ÜŗĶµÄ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶Øµć![]() £¬
£¬![]() £¬Ö±Ļß
£¬Ö±Ļß![]() ”¢
”¢![]() Ļą½»ÓŚµć
Ļą½»ÓŚµć![]() £¬ĒŅĖüĆĒµÄŠ±ĀŹÖ®»żĪŖ
£¬ĒŅĖüĆĒµÄŠ±ĀŹÖ®»żĪŖ![]() £¬¼Ē¶Æµć
£¬¼Ē¶Æµć![]() µÄ¹ģ¼£ĪŖĒśĻß
µÄ¹ģ¼£ĪŖĒśĻß![]() ”£
ӣ
£Ø1£©ĒóĒśĻß![]() µÄ·½³Ģ£»
µÄ·½³Ģ£»
£Ø2£©¹żµć![]() µÄÖ±ĻßÓėĒśĻß
µÄÖ±ĻßÓėĒśĻß![]() ½»ÓŚ
½»ÓŚ![]() ”¢
”¢![]() Į½µć£¬ŹĒ·ń“ęŌŚ¶Øµć
Į½µć£¬ŹĒ·ń“ęŌŚ¶Øµć![]() £¬Ź¹µĆÖ±Ļß
£¬Ź¹µĆÖ±Ļß![]() Óė
Óė![]() Š±ĀŹÖ®»żĪŖ¶ØÖµ£¬Čō“ęŌŚ£¬Ēó³ö
Š±ĀŹÖ®»żĪŖ¶ØÖµ£¬Čō“ęŌŚ£¬Ēó³ö![]() ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ”£
×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖÖ±Ļß![]() ¹żµć
¹żµć![]() £¬Ē抱½ĒĪŖ
£¬Ē抱½ĒĪŖ![]() £¬ŌŚŅŌ×ų±źŌµćĪŖ¼«µć£¬
£¬ŌŚŅŌ×ų±źŌµćĪŖ¼«µć£¬![]() ÖįµÄ·Ēøŗ°ėÖįĪŖ¼«ÖįµÄ¼«×ų±źĻµÖŠ£¬ĒśĻß
ÖįµÄ·Ēøŗ°ėÖįĪŖ¼«ÖįµÄ¼«×ų±źĻµÖŠ£¬ĒśĻß![]() µÄ·½³ĢĪŖ
µÄ·½³ĢĪŖ![]() .
.
£Ø1£©Š“³öÖ±Ļß![]() µÄ²ĪŹż·½³ĢŗĶĒśĻß
µÄ²ĪŹż·½³ĢŗĶĒśĻß![]() µÄÖ±½Ē×ų±ź·½³Ģ£»
µÄÖ±½Ē×ų±ź·½³Ģ£»
£Ø2£©ČōÖ±Ļß![]() ÓėĒśĻß
ÓėĒśĻß![]() Ļą½»ÓŚ
Ļą½»ÓŚ![]() Į½µć£¬Éčµć
Į½µć£¬Éčµć![]() ,Ēó
,Ēó![]() µÄÖµ.
µÄÖµ.
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com