【题目】依照某发展中国家2018年的官方资料，将该国所有家庭按年收入从低到高的顺序平均分为五组，依次为第一组至第五组，各组家庭的年收入总和占该国全部家庭的年收入总和的百分比如图所示.
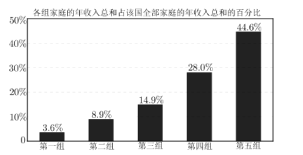
以下关于该国2018年家庭收入的判断，一定正确的是（ ）
A. 至少有
的家庭的年收入都低于全部家庭的平均年收入
B. 收入最低的那
的家庭平均年收入为全部家庭平均年收入的
C. 收入最高的那
的家庭年收入总和超过全部家庭年收入总和的
D. 收入最低的那
的家庭年收入总和超过全部家庭年收入总和的
【答案】C
【解析】
设出所有家庭年收入总和、家庭数，得出所有家庭的平均收入，基于条件“按年收入从低到高的顺序”的情况下，逐一分析各选项的正误， 从而得出结果.
解：设所有家庭年收入总和为100，共有5n个家庭，则所有家庭的平均收入为
，
选项A，第四组、第五组家庭的平均收入均超过
，故极有可能第四组、第五组全部的家庭的收入均超过全部家庭的年平均收入，虽第三组家庭平均年收入为
，由于按年收入从低到高的顺序排列，故仍有可能存在部分家庭年收入超过，这样家庭年收入超过的比率有可能超过
，故A选项不正确；
选项B，收入最低的那
的家庭平均年收入
，为全部家庭平均收入的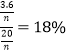
，故选项B不正确；
选项C，收入最高的那
的家庭数应为第四组一半家庭数与第五组家庭数的和，由于按年收入从低到高的顺序排列，故总收入大于
，收入最高的那的家庭年收入总和超过全部家庭年收入总和的
，选项C正确；
选项D，收入最低的那
的家庭数应为第三组家庭数的一半与第一、二组家庭数的和，由于按年收入从低到高的顺序排列，故总收入小于
，收入最低的那的家庭年收入总和不会超过全部家庭年收入总和的，选项D不正确.
故本题选C.
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案科目：高中数学 来源： 题型：
【题目】在平行四边形
中，
，
，过
点作
的垂线，交的延长线于点
，
.连结
，交
于点
，如图1，将
沿折起，使得点到达点
的位置，如图2.
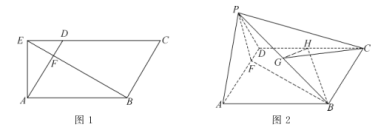
（1）证明：平面
平面
；
（2）若
为
的中点，
为的中点，且平面
平面，求三棱锥
的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】记
表示
，
中的最大值，如
．已知函数
，
．
（1）设
，求函数
在
上零点的个数；
（2）试探讨是否存在实数
，使得
对
恒成立？若存在，求
的取值范围；若不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的离心率为
，以椭圆的上焦点
为圆心，椭圆的短半轴为半径的圆与直线
截得的弦长为
.
（1）求椭圆的方程；
（2）过椭圆左顶点做两条互相垂直的直线
，
，且分别交椭圆于
，
两点（，不是椭圆的顶点），探究直线
是否过定点，若过定点则求出定点坐标，否则说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】不重合的两条直线
，
和不重合的两个平面
，
，下面的几个命题：①若
，且
，则
；②若，与平面成等角，则；③若，
，且
，则；④若，，则
；⑤若，异面，且，均与平面和平行，则.在这5个命题中，真命题的个数是（ ）
A.1B.2C.3D.4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，已知AB为圆O的直径，且
，点D为线段AO的中点，点C为圆O上的一点，且
，
平面ABC，
.
（1）求证：
平面PAB.
（2）求二面角
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
