
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() 为等边三角形,平面
为等边三角形,平面![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点.
的中点.
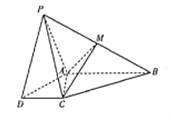
(1)证明:![]() ;
;
(2)求四面体![]() 的体积.
的体积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】依照某发展中国家2018年的官方资料,将该国所有家庭按年收入从低到高的顺序平均分为五组,依次为第一组至第五组,各组家庭的年收入总和占该国全部家庭的年收入总和的百分比如图所示.
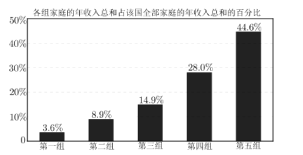
以下关于该国2018年家庭收入的判断,一定正确的是( )
A. 至少有![]() 的家庭的年收入都低于全部家庭的平均年收入
的家庭的年收入都低于全部家庭的平均年收入
B. 收入最低的那![]() 的家庭平均年收入为全部家庭平均年收入的
的家庭平均年收入为全部家庭平均年收入的![]()
C. 收入最高的那![]() 的家庭年收入总和超过全部家庭年收入总和的
的家庭年收入总和超过全部家庭年收入总和的![]()
D. 收入最低的那![]() 的家庭年收入总和超过全部家庭年收入总和的
的家庭年收入总和超过全部家庭年收入总和的![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某居民区有一个银行网点(以下简称“网点”),网点开设了若干个服务窗口,每个窗口可以办理的业务都相同,每工作日开始办理业务的时间是8点30分,8点30分之前为等待时段.假设每位储户在等待时段到网点等待办理业务的概率都相等,且每位储户是否在该时段到网点相互独立.根据历史数据,统计了各工作日在等待时段到网点等待办理业务的储户人数,得到如图所示的频率分布直方图:
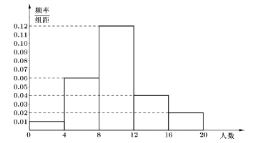
(1)估计每工作日等待时段到网点等待办理业务的储户人数的平均值;
(2)假设网点共有1000名储户,将频率视作概率,若不考虑新增储户的情况,解决以下问题:
①试求每位储户在等待时段到网点等待办理业务的概率;
②储户都是按照进入网点的先后顺序,在等候人数最少的服务窗口排队办理业务.记“每工作日上午8点30分时网点每个服务窗口的排队人数(包括正在办理业务的储户)都不超过3”为事件![]() ,要使事件
,要使事件![]() 的概率不小于0.75,则网点至少需开设多少个服务窗口?
的概率不小于0.75,则网点至少需开设多少个服务窗口?
参考数据:![]() ;
;![]() ;
;
![]() ;
;![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在乎面直角坐标系![]() 中,直线
中,直线![]() :
:![]() (
(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴的非负半轴为极轴,且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴,且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年3月5日,国务院总理李克强作的政府工作报告中,提到要“惩戒学术不端,力戒学术不端,力戒浮躁之风”.教育部日前公布的《教育部2019年部门预算》中透露,2019年教育部拟抽检博士学位论文约6000篇,预算为800万元.国务院学位委员会、教育部2014年印发的《博士硕士学位论文抽检办法》通知中规定:每篇抽检的学位论文送3位同行专家进行评议,3位专家中有2位以上(含2位)专家评议意见为“不合格”的学位论文,将认定为“存在问题学位论文”.有且只有1位专家评议意见为“不合格”的学位论文,将再送2位同行专家进得复评,2位复评专家中有1位以上(含1位)专家评议意见为“不合格”的学位论文,将认定为“存在问题学位论文”.设每篇学位论文被每位专家评议为“不合格”的概率均为![]() ,且各篇学位论文是否被评议为“不合格”相互独立.
,且各篇学位论文是否被评议为“不合格”相互独立.
(1)记一篇抽检的学位论文被认定为“存在问题学位论文”的概率为![]() ,求
,求![]() ;
;
(2)若拟定每篇抽检论文不需要复评的评审费用为900元,需要复评的评审费用为1500元;除评审费外,其它费用总计为100万元.现以此方案实施,且抽检论文为6000篇,问是否会超过预算?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是各项均为正数的等差数列,其中
是各项均为正数的等差数列,其中![]() ,且
,且![]() 成等比数列;数列
成等比数列;数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)如果![]() ,设数列
,设数列![]() 的前
的前![]() 项和为
项和为![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 成立,若存在,求出
成立,若存在,求出![]() 的最小值,若不存在,说明理由.
的最小值,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com