
分析 根据不同情况,利用先分后排的方法,即可得出结论.
解答 解:①小球不同,盒子不同,盒子不空,将小球分成3份,每份1,1,3或1,2,2,再放在3个不同的盒子中,有$(\frac{{C}_{5}^{3}{C}_{2}^{1}}{{A}_{2}^{2}}+\frac{{C}_{5}^{2}{C}_{3}^{2}}{{A}_{2}^{2}})•{A}_{3}^{3}$=150种;
②小球不同,盒子不同,盒子可空,有35种;
③小球不同,盒子相同,盒子不空,将5个不同小球分成3份,分法为1,1,3;1,2,2,共有$\frac{{C}_{5}^{3}{C}_{2}^{1}}{{A}_{2}^{2}}+\frac{{C}_{5}^{2}{C}_{3}^{2}}{{A}_{2}^{2}}$=25种;
④小球不同,盒子相同,盒子可空,将5个不同的小球分成1份、2份、3份,共有${C}_{5}^{5}$+(${C}_{5}^{4}+{C}_{5}^{3}$)+$\frac{{C}_{5}^{3}{C}_{2}^{1}}{{A}_{2}^{2}}+\frac{{C}_{5}^{2}{C}_{3}^{2}}{{A}_{2}^{2}}$=41;
⑤小球相同,盒子不同,盒子不空,用隔板法,有${C}_{4}^{2}$=6种方法;
⑥小球相同,盒子不同,盒子可空,把5个小球及插入的2个隔板都设为小球,7个小球种任选两个变为隔板(可以相邻),那么2块隔板分成3份的小球数对应于相应的3个不同盒子,故有${C}_{7}^{3}$=21种;
⑦小球相同,盒子相同,盒子不空,5个相同的小球分成3份即可,有3,1,1;2,2,1,共2种;
⑧小球相同,盒子相同,只要将5个相同小球分成1份,2份,3份.分法如下:5,0,0;4,1,0;3,2,0;3,1,1;2,2,1,共5种.
点评 本题考查排列组合知识的运用,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,4) | B. | (4,4+2$\sqrt{2}$] | C. | [-4-2$\sqrt{2}$,-4) | D. | [-4-2$\sqrt{2}$,4+2$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
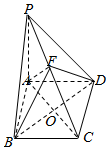 如图,四棱锥P-ABCD的底面ABCD为菱形,PA⊥平面ABCD,PA=AB,∠ABC=60°,点F为PC的中点,则下列说法正确的序号为②④.
如图,四棱锥P-ABCD的底面ABCD为菱形,PA⊥平面ABCD,PA=AB,∠ABC=60°,点F为PC的中点,则下列说法正确的序号为②④.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(2,+∞) | B. | (-2,0)∪(2,+∞) | C. | (-∞,-2)∪(0,2) | D. | (-2,0)∪(0,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com