
| A�� | ��-4��4�� | B�� | ��4��4+2$\sqrt{2}$] | C�� | [-4-2$\sqrt{2}$��-4�� | D�� | [-4-2$\sqrt{2}$��4+2$\sqrt{2}$] |
���� �ȸ������ĵ������Լ��������й�֪ʶ�õ�a+b=1���ٸ��ݻ�������ʽ���$\frac{1}{a}$+$\frac{2}{b}$����Сֵ�����ö����ǹ�ʽ����t=sinx��t��[-1��1]�����캯����f��t��=2t2+mt+2+2$\sqrt{2}$�������ö��κ��������ʷ����������f��t������Сֵ���ٸ��ݴ���Сֵ���ڻ����0�����m�ķ�Χ��
��� �⣺��G�ǡ�ABC�����������ߵĽ��㣬
��$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$��
��$\overrightarrow{GA}$+��a+b��$\overrightarrow{GB}$+c$\overrightarrow{GC}$=$\overrightarrow{0}$��
��1=a+b=c��
��$\frac{1}{a}$+$\frac{2}{b}$=��$\frac{1}{a}$+$\frac{2}{b}$����a+b��=1+2+$\frac{b}{a}$+$\frac{2a}{b}$��3+2$\sqrt{\frac{b}{a}•\frac{2a}{b}}$=3+2$\sqrt{2}$��
���ҽ���a=$\sqrt{2}$-1��b=2-$\sqrt{2}$ʱȡ�Ⱥţ�
��$\frac{1}{a}$+$\frac{2}{b}$��cos2x-msinx��x��R���������
��cos2x-msinx��3+2$\sqrt{2}$��x��R���������
��1-2sin2x-msinx��3+2$\sqrt{2}$��x��R���������
��sinx=t��t��[-1��1]��
��2t2+mt+2+2$\sqrt{2}$��0��[-1��1]�������
��f��t��=2t2+mt+2+2$\sqrt{2}$=2��t+$\frac{m}{2}$��2+2+2$\sqrt{2}$-$\frac{{m}^{2}}{2}$��
��-1��-$\frac{m}{2}$��1����-2��m��2ʱ��f��t��min=2+2$\sqrt{2}$-$\frac{{m}^{2}}{2}$����2+2$\sqrt{2}$-$\frac{{m}^{2}}{2}$��0�����-2��m��2��
��-$\frac{m}{2}$��1ʱ����m��-2ʱ��f��t������СֵΪf��1��=m+4+2$\sqrt{2}$��
����m+4+2$\sqrt{2}$��0�����-4-2$\sqrt{2}$��m��-2
��-$\frac{m}{2}$��-1ʱ����m��2ʱ��f��t������СֵΪf��-1��=-m+4+2$\sqrt{2}$��
����-m+4+2$\sqrt{2}$��0�����2��m��4+2$\sqrt{2}$��
��������m��ȡֵ��ΧΪ[-4-2$\sqrt{2}$��4+2$\sqrt{2}$]��
��ѡ��D
���� ������Ҫ�������ĵ����ʣ������ڼ����е�Ӧ�ã���������ʽ�����κ���������Ӧ�ã�������ת�����������۵���ѧ˼�룬�������⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | R2=1 | B�� | R2=0 | C�� | 0��R2��1 | D�� | R2��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {6��7��8} | B�� | {7��8} | C�� | {5��7��8} | D�� | {5��6��7��8} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
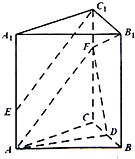 ��ͼ����ֱ������ABC-A1B1C1�У�AA1=AB=AC=3��BC=2��D��BC���е㣬F��CC1��һ�㣬��CF=2��E��AA1��һ�㣬��AE=1��
��ͼ����ֱ������ABC-A1B1C1�У�AA1=AB=AC=3��BC=2��D��BC���е㣬F��CC1��һ�㣬��CF=2��E��AA1��һ�㣬��AE=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
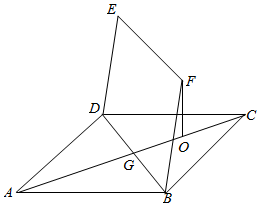 ��ͼ��������ABCD�ı߳�Ϊ2$\sqrt{2}$���ı���BDEF��ƽ���ı��Σ�BD��AC���ڵ�G��OΪGC���е㣬��FO��ƽ��ABCD��FO=$\sqrt{3}$��
��ͼ��������ABCD�ı߳�Ϊ2$\sqrt{2}$���ı���BDEF��ƽ���ı��Σ�BD��AC���ڵ�G��OΪGC���е㣬��FO��ƽ��ABCD��FO=$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com