
分析 运用向量数量积的坐标表示和向量的平方即为模的平方,结合二倍角公式,化简f(x),可得f(x)=2cos2$\frac{x}{2}$-2λcos$\frac{x}{2}$-1,令t=cos$\frac{x}{2}$,$\frac{\sqrt{2}}{2}$≤t≤1,即有y=2t2-2λt-1=2(t-$\frac{1}{2}$λ)2-1+$\frac{1}{2}$λ2,讨论对称轴和区间[$\frac{\sqrt{2}}{2}$,1]的关系,结合单调性,可得最小值,解方程可得所求值.
解答 解:$\overrightarrow{a}$=(cos$\frac{3}{2}$x,sin$\frac{3}{2}$x),$\overrightarrow{b}$=(cos$\frac{x}{2}$,sin$\frac{x}{2}$),
可得$\overrightarrow{a}$•$\overrightarrow{b}$=cos$\frac{3}{2}$xcos$\frac{x}{2}$+sin$\frac{3}{2}$xsin$\frac{x}{2}$=cos($\frac{3}{2}$x-$\frac{1}{2}$x)=cosx,
|$\overrightarrow{a}$+$\overrightarrow{b}$|2=$\overrightarrow{a}$2+$\overrightarrow{b}$2+2$\overrightarrow{a}$•$\overrightarrow{b}$=cos2$\frac{3}{2}$x+sin2$\frac{3}{2}$x+cos2$\frac{x}{2}$+sin2$\frac{x}{2}$+2cosx
=2+2cosx=2•2cos2$\frac{x}{2}$,x∈[0,$\frac{π}{2}$],
即|$\overrightarrow{a}$+$\overrightarrow{b}$|=2cos$\frac{x}{2}$,
则f(x)=$\overrightarrow{a}$$•\overrightarrow{b}$-λ|$\overrightarrow{a}$+$\overrightarrow{b}$|=cosx-2λcos$\frac{x}{2}$
=2cos2$\frac{x}{2}$-2λcos$\frac{x}{2}$-1,
t=cos$\frac{x}{2}$,$\frac{\sqrt{2}}{2}$≤t≤1,
即有y=2t2-2λt-1=2(t-$\frac{1}{2}$λ)2-1+$\frac{1}{2}$λ2,
当$\frac{1}{2}$λ≥1即λ≥2时,函数y在[$\frac{\sqrt{2}}{2}$,1]递减,可得最小值为1-2λ,
由1-2λ=-$\frac{3}{2}$,解得λ=$\frac{5}{4}$<2,不成立;
当$\frac{1}{2}$λ≤$\frac{\sqrt{2}}{2}$即λ≤$\sqrt{2}$时,函数y在[$\frac{\sqrt{2}}{2}$,1]递增,可得最小值为-$\sqrt{2}$λ,
由-$\sqrt{2}$λ=-$\frac{3}{2}$,解得λ=$\frac{3\sqrt{2}}{4}$<$\sqrt{2}$,成立;
当$\frac{\sqrt{2}}{2}$<$\frac{1}{2}$λ<1,即$\sqrt{2}$<λ<2时,函数的最小值为-1+$\frac{1}{2}$λ2=-$\frac{3}{2}$,
可得λ∈∅.
综上可得,λ=$\frac{3\sqrt{2}}{4}$.
故答案为:$\frac{3\sqrt{2}}{4}$.
点评 本题考查向量数量积的坐标表示和性质:向量的平方即为模的平方,考查三角函数的恒等变换,运用换元法和二次函数的最值的求法,以及分类讨论思想方法,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,4) | B. | (4,4+2$\sqrt{2}$] | C. | [-4-2$\sqrt{2}$,-4) | D. | [-4-2$\sqrt{2}$,4+2$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(2,+∞) | B. | (-2,0)∪(2,+∞) | C. | (-∞,-2)∪(0,2) | D. | (-2,0)∪(0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | a3>b3 | C. | $\frac{1}{a-b}$>$\frac{1}{a+b}$ | D. | a4>b4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
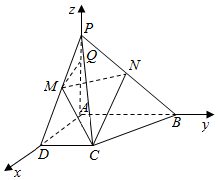 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,PA⊥面ABCD,点Q在棱PA上,且PA=4PQ=4,AB=2,CD=1,AD=$\sqrt{2}$,∠CDA=∠BAD=$\frac{π}{2}$,M,N分别是PD,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,PA⊥面ABCD,点Q在棱PA上,且PA=4PQ=4,AB=2,CD=1,AD=$\sqrt{2}$,∠CDA=∠BAD=$\frac{π}{2}$,M,N分别是PD,PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在厄尔尼诺现象中,经观测,某昆虫的产卵数y与温度x有关,现将收集到的温度xi和产卵数yi(i=1,2,…,7)的7组观测数据作了初步处理,得到如图的散点图及一些统计量表.
在厄尔尼诺现象中,经观测,某昆虫的产卵数y与温度x有关,现将收集到的温度xi和产卵数yi(i=1,2,…,7)的7组观测数据作了初步处理,得到如图的散点图及一些统计量表.| $\overline{x}$ | $\overline{y}$ | $\overline{z}$ | $\sum_{i=1}^{7}$(xi-$\overline{x}$)2 | $\sum_{i=1}^{7}$(xi-$\overline{x}$)(yi-$\overline{y}$) | $\sum_{i=1}^{7}$(xi-$\overline{x}$)(zi-$\overline{z}$) |
| 27.4 | 81.31 | 3.6 | 148 | 2935.13 | 40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com