
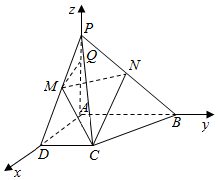
 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,PA⊥面ABCD,点Q在棱PA上,且PA=4PQ=4,AB=2,CD=1,AD=$\sqrt{2}$,∠CDA=∠BAD=$\frac{π}{2}$,M,N分别是PD,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,PA⊥面ABCD,点Q在棱PA上,且PA=4PQ=4,AB=2,CD=1,AD=$\sqrt{2}$,∠CDA=∠BAD=$\frac{π}{2}$,M,N分别是PD,PB的中点.分析 向量法:对于(1)求证:MQ∥平面PCB,可求出线的方向向量与面的法向量,如果两者的内积为0则说明线面平行
对于(2)求截面MCN与底面ABCD所成二面角的大小,求出两个平面的法向量,然后根据根据二面角的正弦与法向量的数量积的关系,求解;
解答 解:法一:向量法:
以A为原点,以AD,AB,AP分别为x,y,z建立空间直角坐标系O-xyz,如图1,
由$AB=2,CD=1,AD=\sqrt{2}$,PA=4PQ=4,M,N分别是PD,PB的中点,
可得:$A({0,0,0}),B({0,2,0}),C({\sqrt{2},1,0}),D({\sqrt{2},0,0}),P({0,0,4}),Q({0,0,3}),M({\frac{{\sqrt{2}}}{2},0,2}),N({0,1,2})$,
∴$\overrightarrow{BC}=({\sqrt{2},-1,0}),\overrightarrow{PB}=({0,2,-4})$,$\overrightarrow{MQ}=({-\frac{{\sqrt{2}}}{2},0,1})$
设平面的PBC的法向量为$\overrightarrow{n_0}=({x,y,z})$,
则有:$\left\{\begin{array}{l}\overrightarrow{n_0}⊥\overrightarrow{BC}⇒({x,y,z})•({\sqrt{2},-1,0})=0⇒\sqrt{2}x-y=0\\ \overrightarrow{n_0}⊥\overrightarrow{PB}⇒({x,y,z})•({0,2,-4})=0⇒2y-4z=0\end{array}\right.$
令z=1,则$x=\sqrt{2},y=2⇒\overrightarrow{n_0}=({\sqrt{2},2,1})$,(3分)
∴$\overrightarrow{MQ}•\overrightarrow{n_0}=({-\frac{{\sqrt{2}}}{2},0,1})•({\sqrt{2},2,1})=0$,
又MQ?平面PCB,∴MQ∥平面PCB;
(2)设平面的MCN的法向量为$\overrightarrow n=({x,y,z})$,又$\overrightarrow{CM}=({-\frac{{\sqrt{2}}}{2},-1,2}),\overrightarrow{CN}=({-\sqrt{2},0,2})$
则有:$\left\{\begin{array}{l}\overrightarrow n⊥\overrightarrow{CM}⇒({x,y,z})•({-\frac{{\sqrt{2}}}{2},-1,2})=0⇒-\frac{{\sqrt{2}}}{2}x-y+2z=0\\ \overrightarrow n⊥\overrightarrow{CN}⇒({x,y,z})•({-\sqrt{2},0,2})=0⇒-\sqrt{2}x+2z=0\end{array}\right.$
令z=1,则$x=\sqrt{2},y=1⇒\overrightarrow n=({\sqrt{2},1,1})$,
又$\overrightarrow{AP}=({0,0,4})$为平面ABCD的法向量,
∴$cos\left?{\overrightarrow n,\overrightarrow{AP}}\right>=\frac{{\overrightarrow n•\overrightarrow{AP}}}{{|{\overrightarrow n}|•|{\overrightarrow{AP}}|}}=\frac{4}{2×4}=\frac{1}{2}$,又截面MCN与底面ABCD所成二面角为锐二面角,
∴截面MCN与底面ABCD所成二面角的大小为$\frac{π}{3}$,
法二:几何法:
(1)取AP的中点E,连接ED,则ED∥CN,如图2,
依题有Q为EP的中点,
所以MQ∥ED,所以MQ∥CN,
又MQ?平面PCB,CN?平面PCB,
∴MQ∥平面PCB
(2)易证:平面MEN∥底面ABCD,
所以截面MCN与平面MEN所成的二面角即为平面MCN与底面ABCD所成的二面角,
因为PA⊥平面ABCD,
所以PA⊥平面MEN,
过E做EF⊥MN,垂足为F,连接QF,
则由三垂线定理可知QF⊥MN,
由(1)可知M,C,N,Q四点共面所以∠QFE为截面MCN与平面MEN所成的二面角的平面角,
$在Rt△MEN中,ME=\frac{{\sqrt{2}}}{2},NE=1,MN=\frac{{\sqrt{6}}}{2},故EF=\frac{{\sqrt{3}}}{3}$,
所以:$tan∠QFE=\sqrt{3}$,
所以:$∠QFE=\frac{π}{3}$;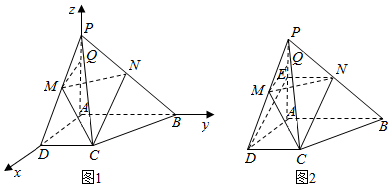
点评 本题考查了线面平行的证明与二面角的求法,是立体几何中一道综合性很强的题,解答本题有一定难度,使用传统的几何法和向量法都可以,体会向量法的思维易而运算难与几何法的思维难而运算易的特征.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1) | B. | [0,2)∪{-$\frac{18}{{e}^{2}}$} | C. | (0,2)∪{-$\frac{18}{{e}^{2}}$} | D. | [0,2$\sqrt{e}$)∪{-$\frac{18}{{e}^{2}}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com