练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．已知函数f（x）=$\frac{2-x}{x-1}$，则函数f（x）的递减区间是（-∞，1），（1，+∞）．

    分析 根据分式函数的性质进行判断求解即可．

    解答 解：f（x）=$\frac{2-x}{x-1}$=$\frac{1-x+1}{x-1}$=-1+$\frac{1}{x-1}$，
    则函数的单调递减区间为（-∞，1），（1，+∞），
    故答案为：（-∞，1），（1，+∞）

    点评 本题主要考查函数单调递减区间的求解，根据分式函数的性质，利用分子常数化进行转化是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    6．已知a，b，c分别是△ABC中角A，B，C的对边，G是△ABC的三条边中线的交点，若$\overrightarrow{GA}$+（a+b）$\overrightarrow{GB}$+c$\overrightarrow{GC}$=$\overrightarrow{0}$，且$\frac{1}{a}$+$\frac{2}{b}$≥cos2x-msinx（x∈R）恒成立，则实数m的取值范围为（　　）
    A．（-4，4）B．（4，4+2$\sqrt{2}$]C．[-4-2$\sqrt{2}$，-4）D．[-4-2$\sqrt{2}$，4+2$\sqrt{2}$]

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．直线$\sqrt{3}$x-ysinθ+2=0的倾斜角的取值范围是[$\frac{π}{3}$，$\frac{2π}{3}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

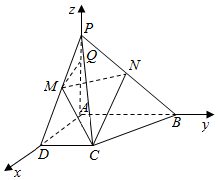    13．如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，PA⊥面ABCD，点Q在棱PA上，且PA=4PQ=4，AB=2，CD=1，AD=$\sqrt{2}$，∠CDA=∠BAD=$\frac{π}{2}$，M，N分别是PD，PB的中点．
    （1）求证：MQ∥面PCB；
    （2）求截面MCN与底面ABCD所成的锐二面角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．已知函数f（x）=|x-1|+|2x-1|+|3x-1|．则f（2）=9，f（x）的最小值为1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知三条直线两两垂直，下列说法正确的是（　　）
    A．这三条直线必共点B．这三条直线不可能在同一平面内
    C．其中必有两条直线异面D．其中必有两条直线共面

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．“函数f（x）=logax（a＞0，a≠1）在其定义域内是减函数”是“loga2＜0”的充要条件（填“充分不必要”“必要不充分”“充要不充分”“充要”“既不充分也不必要”）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．在厄尔尼诺现象中，经观测，某昆虫的产卵数y与温度x有关，现将收集到的温度xi和产卵数yi（i=1，2，…，7）的7组观测数据作了初步处理，得到如图的散点图及一些统计量表．
    $\overline{x}$$\overline{y}$$\overline{z}$$\sum_{i=1}^{7}$（xi-$\overline{x}$）2$\sum_{i=1}^{7}$（xi-$\overline{x}$）（yi-$\overline{y}$）$\sum_{i=1}^{7}$（xi-$\overline{x}$）（zi-$\overline{z}$）
    27.481.313.61482935.1340
    表中zi=lnyi，$\overline{z}$=$\frac{1}{7}$$\sum_{i=1}^{7}$zi．
    （1）根据散点图判断，y=a+bx与y=c1e${\;}^{{c}_{2}x}$哪一个适宜作为y与x之间的回归方程模型？（给出判断即可，不必说明理由）
    （2）根据（1）的判断结果及表中数据．
    ①试求y关于x回归方程；
    ②已知用人工培养该昆虫的成本h（x）与温度x和产卵数y的关系为h（x）=x（lny-9.43）+175，当温度x为何值时，培养成本的预报值最小？
    附：对于一组数据（u1，v1），（u2，v2），…（un，vn），其回归直线v=α+βu的斜率和截距的最小二乘估计分别为β=$\frac{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）（{v}_{i}-\overline{v}）}{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）^{2}}$，α=$\overline{v}$-β$\overline{u}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知二次函数f（x）=ax2+bx+c．
    （1）若f（-1）=0，试判断函数f（x）的零点个数；
    （2）是否存在实数a，b，c，使得f（x）同时满足以下条件：
    ①对?x∈R，f（x-2）=f（-x）；
    ②对?x∈R，0≤f（x）-x≤$\frac{1}{2}$（x-1）2？如果存在，求出a，b，c的值，如果不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案