练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．各种比赛在计算选手最后得分时，要去掉所有评委对该选手所打分数中的最高分和最低分，试设计一个找出最高分的算法．

    分析 可以用循环语句来完成分数的输入，由于每位学生的分数都不小于0分，故我们可以先假设其中的最大数为0，然后每次输入一个学生的分数，就进行一次比较，若输入的数大于0，就将之代替最大数，依次下去，就能找出最大数．

    解答 解：由题意得：
    第一步：令S=0．max=0，i=1
    第二步：比较a（i）与max的大小，如果a（i）＞max，则max=a（i）；
    第三步：是否已经统计每一个学生的成绩，如果是，则执行第四步，如果不是，则i=i+1后，返回第二步
    第四步：输出max的值．

    点评 本题考查的知识点是设计程序框图解决实际问题，分析题意设计出满足条件的算法，并根据框图和语句的功能来实现该算法，是解答本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    11．已知集合P={x∈R|0＜x＜5}，集合Q={x∈R|-1≤x＜3}
    （1）求P∩Q，P∪Q    
    （2）求P∩∁RQ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=lnx-$\frac{1}{2}$ax2+x，a∈R．
    （1）若函数f（x）有极值，求a的取值范围；
    （2）若关于x的不等式f（x）≤ax-1恒成立，求整数a的最小值；
    （3）是否存在x0＞0，使得|f（x）+$\frac{1}{2}{ax}^{2}$-f（x0）|＜x对任意x＞0成立？若存在，求出x0的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．函数f（x）=2sin2x-sin（2x-$\frac{5π}{6}$），x∈R．
    （I）求函数f（x）的最大值，并写出f（x）取最大值时x的取值集合；
    （Ⅱ）若锐角θ满足tanθ=2$\sqrt{2}$，求f（θ）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．函数y=loga（1-ax）在区间[1，2]单调增，则a的取值范围是（0，$\frac{1}{2}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知a、b、c为正数，若a2+b2+4c2=1，求ab+2ac+3$\sqrt{2}$bc的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

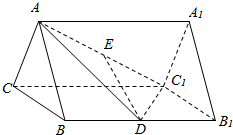    11．在三棱柱ABC-A1B1C1中，△ABC是边长为2正三角形，D、E分别是线段BB1、AC1的中点，DE⊥AC1．
    （1）求证：DE⊥平面AA1C1C；
    （2）若AA1C1C是矩形，BB1=4，求直线BB1与平面ADC1所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知max（a，b）表示a，b两数中的最大值．若f（x）=max{e|x|，e|x-2|}，则f（x）的最小值为e．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知函数f（x）=e1+|x|-$\frac{1}{{1+{x^2}}}$，则使得f（x）＞f（2x-1）成立的x的取值范围是（　　）
    A．$（{\frac{1}{3}，1}）$B．$（{-∞，\frac{1}{3}}）∪（{1，+∞}）$C．（-$\frac{1}{3}$，$\frac{1}{3}$）D．$（{-∞，-\frac{1}{3}}）∪（{\frac{1}{3}，+∞}）$

    查看答案和解析>>

    同步练习册答案