
���� ��������ķ��жϢٵ�����д������ķ������жϢڵ��������ó�Ҫ�����жϢۢܵ�����
��� �⣺�����⡰?x0��R��x${\;}_{0}^{2}$-1��0���ķ��ǡ�?x��R��x2-1��0������������ķ���ʽ��ȷ��
�����⡰��x=3����x2-2x-3=0���ķ������ǡ���x��3����x2-2x-3��0�������������Ķ��壬��ȷ��
����a��b��R����log${\;}_{\frac{1}{2}}$a��log${\;}_{\frac{1}{2}}$b����֪0��a��b���ɵá�3a��3b�������ǡ�3a��3b����֪a��b�������Ƴ���log${\;}_{\frac{1}{2}}$a��log${\;}_{\frac{1}{2}}$b�������ԡ�log${\;}_{\frac{1}{2}}$a��log${\;}_{\frac{1}{2}}$b���ǡ�3a��3b���dz�ֲ���Ҫ���������Ԣ۲���ȷ��
�ܡ�cosx=cosy���ǡ�x=��y+2k�У�k��Z���ij�Ҫ���������Ԣܲ���ȷ��
�ʴ�Ϊ���٢ڣ�
���� ���⿼���������ٵ��ж���Ӧ�ã���Ҫ�����Լ�����ķ��������������ϵ���ǻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��x�������ֵΪ2 | B�� | f��x�������ֵΪ3 | C�� | f��x������СֵΪ2 | D�� | f��x������СֵΪ3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | p2��p3 | B�� | p2��p4 | C�� | p1��p3 | D�� | p1��p4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
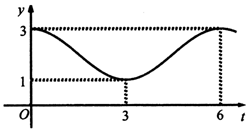 ij�����мס������������䣬����ˮ˲ʱ�ŷ���y����λ��m3/h ������ʱ��t����λ��h���Ĺ�ϵ�����Ƶ����㺯��y=Asin����t+�գ�+b��A��0���أ�0��0���գ��У�����ͼ�����£�
ij�����мס������������䣬����ˮ˲ʱ�ŷ���y����λ��m3/h ������ʱ��t����λ��h���Ĺ�ϵ�����Ƶ����㺯��y=Asin����t+�գ�+b��A��0���أ�0��0���գ��У�����ͼ�����£��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com