
分析 (1)根据条件得到关于a,b的方程组解的求出k,b的值,得到函数P=-t+60,代值计算即可,
(2)由条件得到日销售额y的函数关系式,分段,根据二次函数的性质即可求出.
解答 解:(1)因为P=kt+b
所以$\left\{\begin{array}{l}55=5t+b\\ 50=10t+b\end{array}\right.$
得:k=-1,b=60即:P=-t+60
当t=20时,P=40
答:第20日的销售量为40件,
(2)$y=PQ=\left\{\begin{array}{l}(t+20)(-t+60),1≤t<25\\(80-t)(-t+60),25≤t≤30\end{array}\right.(t∈{N^+})$,
═$\left\{\begin{array}{l}-{t^2}+40t+120,1≤t<25\\{t^2}-140t+480,25≤t≤30\end{array}\right.(t∈{N^+})$,
当1≤t<25时,y=-t2+40t+120=-(t-20)2+1600
即t=20时,y取得最大值1600,
当25≤t≤30时,y=t2-140t+480=(t-70)2-10
即t=25时,y取得最大值2395,
综上,当t=25时,日销售额y的最大值为2395元
答:日销售额y的最大值为2395元.
点评 本题考查了一次函数,二次函数的图象与性质,以及简单的作图能力,归纳猜想能力,是中档题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:选择题
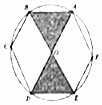 已知正六边形ABCDEF内接于圆O,连接AD,BE,现在往圆O内投掷2000粒小米,则可以估计落在阴影区域内的小米的粒数大致是( )(参考数据:$\frac{π}{\sqrt{3}}$=1.82,$\frac{\sqrt{3}}{π}$=0.55)
已知正六边形ABCDEF内接于圆O,连接AD,BE,现在往圆O内投掷2000粒小米,则可以估计落在阴影区域内的小米的粒数大致是( )(参考数据:$\frac{π}{\sqrt{3}}$=1.82,$\frac{\sqrt{3}}{π}$=0.55)| A. | 550 | B. | 600 | C. | 650 | D. | 700 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,2,3} | B. | {-2,1,2,3} | C. | {-1,0,2,3} | D. | {2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
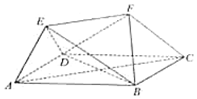 如图,在多面体ABCDEF中,底面ABCD是菱形,AB=2,∠DAB=60°,EF∥AC,EF=$\sqrt{3}$.
如图,在多面体ABCDEF中,底面ABCD是菱形,AB=2,∠DAB=60°,EF∥AC,EF=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 物理成绩 | 65 | 70 | 75 | 81 | 85 | 87 | 93 |
| 化学成绩 | 72 | 68 | 80 | 85 | 90 | 86 | 91 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com