
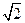 ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.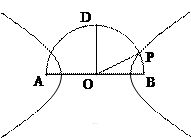
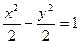 .(Ⅱ)直线l的斜率的取值范围是[-
.(Ⅱ)直线l的斜率的取值范围是[-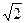 ,-1)
,-1)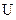 (-1,1)
(-1,1)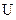 (1,
(1,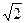 ]. ;
]. ;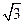 ,1).
,1). 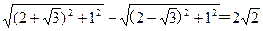 ,2c=|AB|=4.
,2c=|AB|=4. 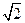 ,c=2,从而b2=c2-a2=2.
,c=2,从而b2=c2-a2=2. 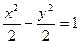 .
. 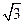 ,1).
,1). 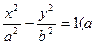 >0,b>0),则
>0,b>0),则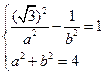 .
. 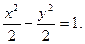
 ,
,
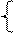
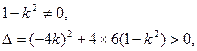 即
即 
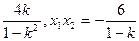 .
. 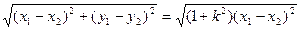
 .
. 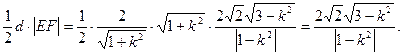
 ,则
,则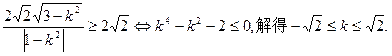
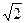 ,-1)
,-1)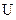 (-1,1)
(-1,1)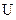 (1,
(1,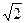 ].
]. 

 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源:不详 题型:解答题
 椭圆方程为
椭圆方程为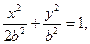 抛物线方程为
抛物线方程为 如图4所示,过点
如图4所示,过点 作
作 轴的平行线,与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点
轴的平行线,与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点
 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标) 。
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标) 。
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
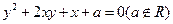 to the y-axis is
to the y-axis is  then the velue of a is
then the velue of a isA.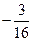 | B.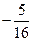 | C.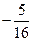 or or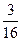 | D.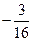 or or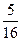 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
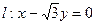 与曲线
与曲线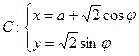
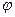 为参数,
为参数,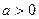 )有两个公共点A,B,且|AB|=2,则实数a的值为 ;在此条件下,以直角坐标系的原点为极点,x轴正方向为极轴建立坐标系,则曲线C的极坐标方程为 .
)有两个公共点A,B,且|AB|=2,则实数a的值为 ;在此条件下,以直角坐标系的原点为极点,x轴正方向为极轴建立坐标系,则曲线C的极坐标方程为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com