
分析 (1)基本量法,即用a1,d表示S10,列出关于d的方程,解出d,即可求数列{an}的通项公式;
(2)由平方降幂公式及二倍角公式、两角和与差的正弦公式化简函数解析式可得$f(x)=2sin(2x+\frac{π}{3})$,由-$\frac{π}{6}≤x≤\frac{π}{3}$可得0$≤2x+\frac{π}{3}≤π$,由三角函数性质可求出值域.
解答 解:(1)由题意得设数列{an}的公差为d,
此时${S}_{10}=\frac{10({a}_{1}+{a}_{10})}{2}$=$\frac{10({a}_{1}+{a}_{1}+9d)}{2}$=120,
解得d=2,
∴an=a1+(n-1)d=2n+1.
(2)∵f(x)=2$\sqrt{3}sinxcosx+2co{s}^{2}x-1$
=$\sqrt{3}sin2x+cos2x$=2sin(2x+$\frac{π}{6}$),-$\frac{π}{6}≤x≤\frac{π}{3}$,
又-$\frac{π}{6}≤x≤\frac{π}{3}$,从而-$\frac{π}{6}$≤2x+$\frac{π}{6}$≤$\frac{5π}{6}$,
∴2x+$\frac{π}{6}$=0时,f(x)min=0,2x+$\frac{π}{6}=\frac{π}{2}$时,f(x)max=2,
故函数f(x)的值域为[0,2].
点评 本题考查数列的通项的求法,考查函数的值域的求法,是中档题,解题时要认真审题,注意等差数列及函数性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 36 | C. | 48 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\sqrt{2}$ | B. | $±\sqrt{3}$ | C. | ±1 | D. | ±2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
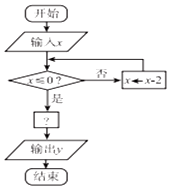 如图是一个算法的程序框图,当输入的x的值为7时,输出的 y值恰好是-1,则“?”处应填的关系式可能是( )
如图是一个算法的程序框图,当输入的x的值为7时,输出的 y值恰好是-1,则“?”处应填的关系式可能是( )| A. | y=2x+1 | B. | y=3-x | C. | y=|x| | D. | y=log${\;}_{\frac{1}{3}}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,五面体ABCDE,四边形ABDE是矩形,△ABC是正三角形,AB=1,AE=2,F是线段BC上一点,直线BC与平面ABD所成角为30°,CE∥平面ADF.
如图,五面体ABCDE,四边形ABDE是矩形,△ABC是正三角形,AB=1,AE=2,F是线段BC上一点,直线BC与平面ABD所成角为30°,CE∥平面ADF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (5,5) | B. | (-1,1) | C. | (5,5)或(-1,1) | D. | (5,5)或(1,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com