
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC= ![]() ,AB=1,BD=PA=2,M 为PD的中点.
,AB=1,BD=PA=2,M 为PD的中点. 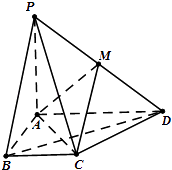
(1)求异面直线BD与PC所成角的余弦值;
(2)求二面角A﹣MC﹣D的平面角的余弦值.
【答案】
(1)解:∵PA⊥平面ABCD,AB平面ABCD,AD平面ABCD,
∴PA⊥AB,PA⊥AD.又AD⊥AB,如图,以AB,AD,AP所在直线为x轴、y轴、z轴建立空间直角坐标系.
根据条件得AD= ![]() ,∴B(1,0,0),D(0,
,∴B(1,0,0),D(0, ![]() ,0),C
,0),C ![]() ,P(0,0,2),
,P(0,0,2),
则 ![]() =(﹣1,
=(﹣1, ![]() ,0),
,0), ![]() =
= ![]() .
.
设异面直线BD,PC所成的角为θ,
则cos θ=|cos< ![]() >|=
>|= 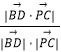 =
= ![]() =
= ![]() .
.
即异面直线BD与PC所成角的余弦值为 ![]() .
.
(2)解:设平面AMC的一个法向量为n1=(x1,y1,z1), ![]() ,
, ![]()
则n1⊥ ![]() ,∴n1
,∴n1 ![]() =(x1,y1,z1)
=(x1,y1,z1) ![]() =
= ![]() ,
,
又n1⊥ ![]() ,∴n1
,∴n1 ![]() =(x1,y1,z1)
=(x1,y1,z1) ![]() =
= ![]() ,
,
取y1=- ![]() ,得x1=2,z1=
,得x1=2,z1= ![]() ,故n1=(2,-
,故n1=(2,- ![]() ,
, ![]() ),
),
同理可得平面BMC的一个法向量n2=(1, ![]() ,
, ![]() ),
),
∵cos<n1,n2>= 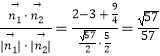 ,
,
∴二面角A﹣MC﹣D的平面角的余弦值为 ![]() .
.
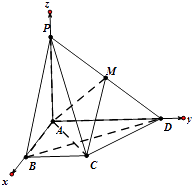
【解析】(1)建立空间直角坐标系,利用向量的夹角公式即可得出异面直线所成的角.(2)利用法向量的性质、线面垂直的性质、向量的夹角公式即可得出.
【考点精析】根据题目的已知条件,利用异面直线及其所成的角的相关知识可以得到问题的答案,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】已知:f(x)=2 ![]() cos2x+sin2x﹣
cos2x+sin2x﹣ ![]() +1(x∈R).求:
+1(x∈R).求:
(1)f(x)的最小正周期;
(2)f(x)的单调增区间;
(3)若x∈[﹣ ![]() ,
, ![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x||x﹣a|≤3,x∈R},B={x|x2﹣3x﹣4>0,x∈R}.
(1)若a=1,求A∩B;
(2)若A∪B=R,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为整数的数列{an}满足an2≤1,1≤a12+a22+…+an2≤m,m,n∈N* .
(1)若m=1,n=2,写出所有满足条件的数列{an};
(2)设满足条件的{an}的个数为f(n,m).
①求f(2,2)和f(2016,2016);
②若f(m+1,m)>2016,试求m的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某影院为了宣传影片《战狼Ⅱ》,准备采用以下几种方式来扩大影响,吸引市民到影院观看影片,根据以往经验,预测:
①分发宣传单需要费用1.5万元,可吸引30%的市民,增加收入4万元;
②网络上宣传,需要费用8千元,可吸引20%的市民,增加收入3万元;
③制作小视频上传微信群,需要费用2.5万元,可吸引35%的市民,增加收入5.5万元;
④与商场合作需要费用1万元,购物满800元者可免费观看影片(商场购票),可吸收15%的市民,增加收入2.5万元,
问: (1)在三个观看影片的市民中,至少有一个是通过微信群宣传方式吸引来的概率是多少?
(2)影院预计可增加盈利是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m,n∈R,定义在区间[m,n]上的函数f(x)=log2(4﹣|x|)的值域是[0,2],若关于t的方程( ![]() )|t|+m+1=0(t∈R)有实数解,则m+n的取值范围是 .
)|t|+m+1=0(t∈R)有实数解,则m+n的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆. 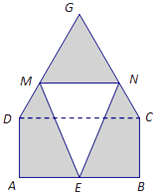
(1)设MN与AB之间的距离为x米,试将△EMN的面积S(平方米)表示成关于x的函数;
(2)求△EMN的面积S(平方米)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,
(单位:元),继续购买该险种的投保人称为续保人,
续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
随机调查了该险种的400名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 |
|
频数 | 120 | 100 | 60 | 60 | 40 | 20 |
(Ⅰ)记A为事件:“一续保人本年度的保费不高于基本保费”.求![]() 的估计值;
的估计值;
(Ⅱ)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的190%”.
求![]() 的估计值;
的估计值;
(III)求续保人本年度的平均保费估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)定义域中任意的x1 , x2(x1≠x2),有如下结论:
①f(x1+x2)=f(x1)f(x2);
②f(x1x2)=f(x1)+f(x2);
③ ![]() >0;
>0;
④ ![]() .
.
当f(x)=lgx时,上述结论中正确结论的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com