
【题目】对于函数f(x)定义域中任意的x1 , x2(x1≠x2),有如下结论:
①f(x1+x2)=f(x1)f(x2);
②f(x1x2)=f(x1)+f(x2);
③ ![]() >0;
>0;
④ ![]() .
.
当f(x)=lgx时,上述结论中正确结论的序号是 .
【答案】②③
【解析】解:①f(x1+x2)=lg(x1+x2)≠f(x1)f(x2)=lgx1lgx2
②f(x1x2)=lgx1x2=lgx1+lgx2=f(x1)+f(x2)
③f(x)=lgx在(0,+∞)单调递增,则对任意的0<x1<x2 , d都有f(x1)<f(x2)
即 ![]()
④ ![]() ,
, ![]() =
= ![]()
∵ ![]() ∴
∴ ![]()
所以答案是:②③
【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识,掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较,以及对函数的奇偶性的理解,了解偶函数的图象关于y轴对称;奇函数的图象关于原点对称.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC= ![]() ,AB=1,BD=PA=2,M 为PD的中点.
,AB=1,BD=PA=2,M 为PD的中点. 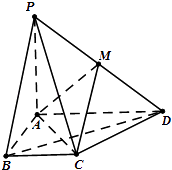
(1)求异面直线BD与PC所成角的余弦值;
(2)求二面角A﹣MC﹣D的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级体育课举行了一次“投篮比赛”活动,为了了解本次投篮比赛学生总体情况,从中抽取了甲乙两个小组样本分数的茎叶图如图所示.
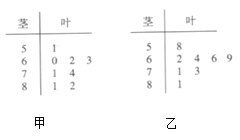
(1)分别求出甲乙两个小组成绩的平均数与方差,并判断哪一个小组的成绩更稳定:
(2)从甲组成绩不低于60分的同学中,任意抽取3名同学,设![]() 表示所抽取的3名同学中得分在
表示所抽取的3名同学中得分在![]() 的学生个数,求
的学生个数,求![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品在近30天内每件的销售价格P(元)与时间t(天)的函数是:P= ![]()
该商品的日销售量Q(件)与时间t(天)的函数关系是:Q=﹣t+40(0<t≤30,t∈N*),求这种商品的日销售金额的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z1=(1+bi)(2+i),z2=3+(1﹣a)i(a,b∈R,i为虚数单位).
(1)若z1=z2 , 求实数a,b的值;
(2)若b=1,a=0,求| ![]() |.
|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com