
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,证明:
时,证明:![]() ;
;
(3)试比较![]() 与
与![]()
![]() ,并证明你的结论。
,并证明你的结论。
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)求得![]() ,对
,对![]() 的范围分类讨论即可求得
的范围分类讨论即可求得![]() 的单调性。
的单调性。
(2)将![]() 转化成
转化成![]() ,证明
,证明![]() 恒成立,利用导数求得
恒成立,利用导数求得![]() ,问题得证。
,问题得证。
(3)由(2)可得:![]() ,整理得:
,整理得:![]() ,所以
,所以![]() ,整理
,整理![]() 得:
得:![]()
利用![]() 即可得:
即可得:![]() ,问题得解。
,问题得解。
(1)函数![]() 的定义域为:
的定义域为:![]() ,
,![]()
![]()
①当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增
上单调递增
②当![]() 时,令
时,令![]() ,解得
,解得![]()
![]() .
.
当![]() 时,
时,![]() ,所以
,所以![]() , 所以
, 所以![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
综上,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)当![]()
![]() 时,
时,![]() ,要证明
,要证明![]() ,
,
即证![]() ,即证:
,即证:![]() .
.
设![]() ,则
,则![]()
![]() ,令
,令![]() 得,
得,![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
所以![]() 为极大值点,且
为极大值点,且![]() 在
在![]() 处取得最大值。
处取得最大值。
所以![]() ,即
,即![]() 。故
。故![]() .
.
(3)证明:![]() (当且仅当
(当且仅当![]() 时等号成立),即
时等号成立),即![]() ,
,
则有![]() +
+![]()
![]()
![]() ,
,
故:![]() +
+![]()


科目:高中数学 来源: 题型:
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表:
列联表:
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)判断能否有![]() 的把握认为是否生二孩与头胎的男女情况有关;附:
的把握认为是否生二孩与头胎的男女情况有关;附:
| 0,15 | 0.05 | 0.01 | 0.0012.0 |
k | 2.072 | 3.841 | 6.635 | 10.828 |
 (其中
(其中![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 在线段
在线段![]() 上运动,则下列判断中正确的是( )
上运动,则下列判断中正确的是( )
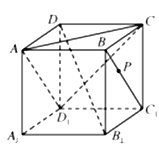
①平面![]() 平面
平面![]() ;
;
②![]() 平面
平面![]() ;
;
③异面直线![]() 与
与![]() 所成角的取值范围是
所成角的取值范围是![]() ;
;
④三棱锥![]() 的体积不变.
的体积不变.
A. ①② B. ①②④ C. ③④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据以往的经验,某工程施工期间的降水量![]() (单位:
(单位:![]() )对工期的影响如下表:
)对工期的影响如下表:
降水量 |
|
|
|
|
工期延误天数 |
|
|
|
|
历年气象资料表明,该工程施工期间降水量![]() 小于
小于![]() 、
、![]() 、
、![]() 的概率分别为
的概率分别为![]() 、
、![]() 、
、![]() ,求:
,求:
(1)在降水量![]() 至少是
至少是![]() 的条件下,工期延误不超过
的条件下,工期延误不超过![]() 天的概率;
天的概率;
(2)工期延误天数![]() 的均值与方差.
的均值与方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-ABCD中,平面![]() 垂直于对角线AC,且平面
垂直于对角线AC,且平面![]() 截得正方体的六个表面得到截面六边形,记此截面六边形的面积为S,周长为l,则( )
截得正方体的六个表面得到截面六边形,记此截面六边形的面积为S,周长为l,则( )
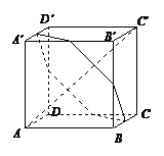
A. S为定值,l不为定值 B. S不为定值,l为定值
C. S与l均为定值 D. S与l均不为定值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com