
【题目】如图,AOB是一块半径为r的扇形空地,![]() .某单位计划在空地上修建一个矩形的活动场地OCDE及一矩形停车场EFGH,剩余的地方进行绿化.若
.某单位计划在空地上修建一个矩形的活动场地OCDE及一矩形停车场EFGH,剩余的地方进行绿化.若![]() ,设
,设![]()
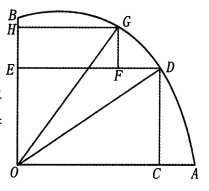
(Ⅰ)记活动场地与停车场占地总面积为![]() ,求
,求![]() 的表达式;
的表达式;
(Ⅱ)当![]() 为何值时,可使活动场地与停车场占地总面积最大.
为何值时,可使活动场地与停车场占地总面积最大.
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.

(Ⅰ)证明: BC1//平面A1CD;
(Ⅱ)设AA1= AC=CB=2,AB=2![]() ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆![]() :
:![]() .
.

(Ⅰ)若圆C与x轴相切,求圆C的方程;
(Ⅱ)已知![]() ,圆
,圆![]() 与x轴相交于两点
与x轴相交于两点![]() (点
(点![]() 在点
在点![]() 的左侧).过点
的左侧).过点![]() 任作一条直线与圆
任作一条直线与圆![]() :
:![]() 相交于两点A,B.问:是否存在实数a,使得
相交于两点A,B.问:是否存在实数a,使得![]() =
=![]() ?若存在,求出实数a的值,若不存在,请说明理由.
?若存在,求出实数a的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某果农从经过筛选(每个水果的大小最小不低于50克,最大不超过100克)的10000个水果中抽取出100个样本进行统计,得到如下频率分布表:
级别 | 大小(克) | 频数 | 频率 |
一级果 |
| 5 | 0.05 |
二级果 |
|
| |
三级果 |
| 35 |
|
四级果 |
| 30 | |
五级果 |
| 20 | |
合计 | 100 |
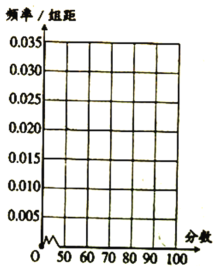
请根据频率分布表中所提供的数据,解得下列问题:
(1)求![]() 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;
(2)若从四级果,五级果中按分层抽样的方法抽取5个水果,并从中选出2个作为展品,求2个展品中仅有1个是四级果的概率;
(3)若将水果作分级销售,预计销售的价格![]() 元/个与每个水果的大小
元/个与每个水果的大小![]() 克关系是:
克关系是: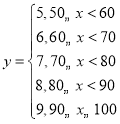 ,则预计10000个水果可收入多少元?
,则预计10000个水果可收入多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋数学家杨辉所著的![]() 详解九章算术
详解九章算术![]() 一书中,用图
一书中,用图![]() 的数表列出了一些正整数在三角形中的一种几何排列,俗称“杨辉三角形”,该数表的规律是每行首尾数字均为1,从第三行开始,其余的数字是它“上方”左右两个数字之和
的数表列出了一些正整数在三角形中的一种几何排列,俗称“杨辉三角形”,该数表的规律是每行首尾数字均为1,从第三行开始,其余的数字是它“上方”左右两个数字之和![]() 现将杨辉三角形中的奇数换成1,偶数换成0,得到图
现将杨辉三角形中的奇数换成1,偶数换成0,得到图![]() 所示的由数字0和1组成的三角形数表,由上往下数,记第n行各数字的和为
所示的由数字0和1组成的三角形数表,由上往下数,记第n行各数字的和为![]() ,如
,如![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]()
![]()

A. 2 B. 4 C. 8 D. 16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某批发市场一服装店试销一种成本为每件![]() 元的服装规定试销期间销售单价不低于成本单价,且获利不得高于成本的
元的服装规定试销期间销售单价不低于成本单价,且获利不得高于成本的![]() ,经试销发现销售量
,经试销发现销售量![]() (件)与销售单价
(件)与销售单价![]() (元)符合一次函数
(元)符合一次函数![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
(1)求一次函数![]() 的解析式,并指出
的解析式,并指出![]() 的取值范围;
的取值范围;
(2)若该服装店获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式;销售单价
之间的关系式;销售单价![]() 定为多少元时,可获得最大利润最大利润是多少元?
定为多少元时,可获得最大利润最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com