【题目】将一枚硬币抛10次，那么至少连续5次都出现正面的不同情形共______种。
【答案】112
【解析】
如果刚好有5次连续正面向上，分成三类，第一类，5次正面向上的前后各有一次反面向上，有
种；第二类，5次正面向上在最后，前面一次反面向上，有
种；第三类，5次正面向上在最前面，后面一次反面向上，有种，共有64种方法.
如果刚好有6次连续正面向上，分成三类，第一类，6次正面向上的前后各有一次反面向上，有
种；第二类，6次正面向上在最后，前面一次反面向上，有
种；第三类，6次正面向上在最前面，后面一次反面向上，有种，共有28种方法.
如果刚好有7次连续正面向上，分成三类，第一类，7次正面向上的前后各有一次反面向上，有
种；第二类，7次正面向上在最后，前面一次反面向上，有
种；第三类，7次正面向上在最前面，后面一次反面向上，有种，共有12种方法.
如果刚好有8次连续正面向上，分成三类，第一类，8次正面向上的前后各有一次反面向上，有1种；第二类，8次正面向上在最后，前面一次反面向上，有
种；第三类，8次正面向上在最前面，后面一次反面向上，有2种，共有5种方法.
如果刚好有9次连续正面向上，共有2种方法.
如果刚好有10次连续正面向上，共有1种方法.
综上所述共有64+28+12+5+2+1=112种.
故答案为：112
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】如图，AOB是一块半径为r的扇形空地，
．某单位计划在空地上修建一个矩形的活动场地OCDE及一矩形停车场EFGH，剩余的地方进行绿化．若
，设
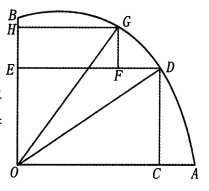
(Ⅰ)记活动场地与停车场占地总面积为
，求的表达式；
(Ⅱ)当
为何值时，可使活动场地与停车场占地总面积最大．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在平面直角坐标系
中，设点
，直线
:
，点
在直线上移动，
是线段
与
轴的交点,过、分别作直线
、
，使
，
，
.
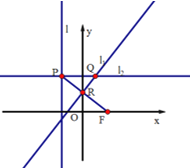
(1)求动点
的轨迹
的方程；
(2)已知⊙
：
，过抛物线上一点
作两条直线与⊙相切于
、
两点，若直线
在轴上的截距为
，求的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，已知圆C1：(x＋3)2＋(y－1)2＝4和圆C2：(x－4)2＋(y－5)2＝4.
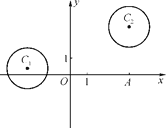
(1)若直线l过点A(4，0)，且被圆C1截得的弦长为2
，求直线l的方程；
(2)设P为平面上的点，满足：存在过点P的无穷多对互相垂直的直线l1和l2，它们分别与圆C1和圆C2相交，且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等，试求所有满足条件的点P的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设
。
，
，
，
是
中的数所成的数列，它包含的不以1结尾的任何排列，即对于的四个数的任意一个不以1结尾的排列
，
，都有
，
，
，
，使得
，并且
，求这种数列的项数
的最小值。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设有关于
的一元二次方程
．
（Ⅰ）若
是从
四个数中任取的一个数，
是从
三个数中任取的一个数，求上述方程有实根的概率．
（Ⅱ）若是从区间
任取的一个数，是从区间
任取的一个数，求上述方程有实根的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
