【题目】我国南宋数学家杨辉所著的
详解九章算术
一书中，用图
的数表列出了一些正整数在三角形中的一种几何排列，俗称“杨辉三角形”，该数表的规律是每行首尾数字均为1，从第三行开始，其余的数字是它“上方”左右两个数字之和
现将杨辉三角形中的奇数换成1，偶数换成0，得到图
所示的由数字0和1组成的三角形数表，由上往下数，记第n行各数字的和为
，如
，
，
，
，
，则
A. 2 B. 4 C. 8 D. 16
科目：高中数学 来源： 题型：
【题目】已知圆锥的顶点为
，底面圆心为
，半径为
．
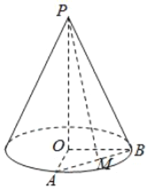
（1）设圆锥的母线长为
，求圆锥的体积；
（2）设
，
、
是底面半径，且
，
为线段
的中点，如图．求异面直线
与所成的角的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，AOB是一块半径为r的扇形空地，
．某单位计划在空地上修建一个矩形的活动场地OCDE及一矩形停车场EFGH，剩余的地方进行绿化．若
，设
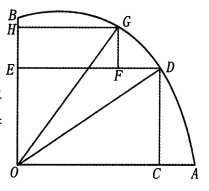
(Ⅰ)记活动场地与停车场占地总面积为
，求的表达式；
(Ⅱ)当
为何值时，可使活动场地与停车场占地总面积最大．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系中，方程
（为
，
为不相等的两个正数）所代表的曲线是（ ）
A. 三角形 B. 正方形 C. 非正方形的长方形 D. 非正方形的菱形
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
： 
的左、右焦点分别为
和
，离心率是
，直线
过点
交椭圆于
， 
两点，当直线
过点
时， 
的周长为
.
（Ⅰ）求椭圆
的标准方程；
（Ⅱ）当直线
绕点
运动时，试求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在平面直角坐标系
中，设点
，直线
:
，点
在直线上移动，
是线段
与
轴的交点,过、分别作直线
、
，使
，
，
.
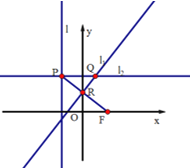
(1)求动点
的轨迹
的方程；
(2)已知⊙
：
，过抛物线上一点
作两条直线与⊙相切于
、
两点，若直线
在轴上的截距为
，求的最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
