[题目]已知函数若函数存在5个零点.则实数的取值范围为 . 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知函数若函数存在5个零点，则实数的取值范围为________.

【答案】

【解析】

先作出函数y=2f(x)的图像，再令=0，则存在5个零点，再作函数y=的图像，数形结合分析得到a的取值范围.

先作出函数y=2f(x)的图像如图所示(图中黑色的曲线)，

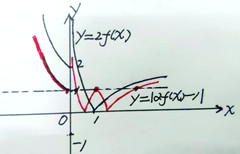
当a=1时，函数y=|2f(x)-1|的图像如图所示（图中红色的曲线），它与直线y=1只有四个交点，即函数存在4个零点，不合题意.

当1＜a＜3时，函数y=|2f(x)-a|的图像如图所示（图中红色的曲线），它与直线y=1有5个交点，即函数存在5个零点，符合题意.

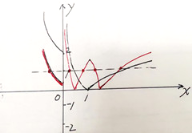
当a=3时，函数y=|2f(x)-3|的图像如图所示（图中红色的曲线），它与直线y=1有6个交点，即函数存在6个零点，不符合题意.

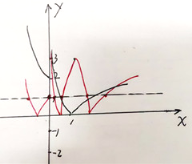
所以实数a的取值范围为.

故答案为：

练习册系列答案

创新考王完全试卷系列答案

期末复习检测系列答案

超能学典单元期中期末专题冲刺100分系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知是椭圆：（）与抛物线:的一个公共点，且椭圆与抛物线具有一个相同的焦点．

（Ⅰ）求椭圆及抛物线的方程；

（Ⅱ）设过且互相垂直的两动直线，与椭圆交于两点，与抛物线交于两点，求四边形面积的最小值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆的左、右焦点分别为，离心率，且椭圆的短轴长为2.

（1）球椭圆的标准方程；

（2）已知直线过右焦点，且它们的斜率乘积为，设分别与椭圆交于点和.

①求的值；

②设的中点，的中点为，求面积的最大值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】有一种鱼的身体吸收汞，一定量身体中汞的含量超过其体重的1.00ppm（即百万分之一）的鱼被人食用后，就会对人体产生危害.在30条鱼的样本中发现的汞含量（单位：ppm）如下：

0.07 0.24 0.95 0.98 1.02 0.98 1.37 1.40 0.39 1.02

1.44 1.58 0.54 1.08 0.61 0.72 1.20 1.14 1.62 1.68

1.85 1.20 0.81 0.82 0.84 1.29 1.26 2.10 0.91 1.31

（1）请用合适的统计图描述上述数据，并分析这30条鱼的汞含量的分布特点；

（2）求出上述样本数据的平均数和标准差；

（3）从实际情况看，许多鱼的汞含量超标的原因是这些鱼在出售之前没有被检测过你认为每批这种鱼的平均承含量都比1.00ppm大吗？

（4）在上述样本中，有多少条鱼的汞含量在以平均数为中心、2倍标准差的范围内？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】年诺贝尔生理学或医学奖获得者威廉·凯林（WilliamG.KaelinJr）在研究肾癌的抑制剂过程中使用的输液瓶可以视为两个圆柱的组合体.开始输液时，滴管内匀速滴下液体（滴管内液体忽略不计），设输液开始后分钟，瓶内液面与进气管的距离为厘米，已知当时，.如果瓶内的药液恰好分钟滴完.则函数的图像为（）