
【题目】已知函数 与
与![]() ,若对任意的
,若对任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,则实数
,则实数![]() 的取值范围是______.
的取值范围是______.
【答案】![]()
【解析】
求出函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,由题意可知,由
,由题意可知,由![]() ,可得出
,可得出![]() ,由题意知,函数
,由题意知,函数![]() 在区间
在区间![]() 上的值域包含
上的值域包含![]() ,然后对
,然后对![]() 分
分![]() 、
、![]() 、
、![]() 三种情况分类讨论,求出函数
三种情况分类讨论,求出函数![]() 在区间
在区间![]() 上的值域,可得出关于实数
上的值域,可得出关于实数![]() 的不等式(组),解出即可.
的不等式(组),解出即可.
由于函数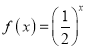 在
在![]() 上的减函数,则
上的减函数,则![]() ,即
,即![]() ,
,
所以,函数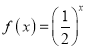 在区间
在区间![]() 上的值域为
上的值域为![]() .
.
对于函数![]() ,内层函数为
,内层函数为![]() ,外层函数为
,外层函数为![]() .
.
令![]() ,得
,得![]() .
.
由题意可知,函数![]() 在区间
在区间![]() 上的值域包含
上的值域包含![]() .
.
函数![]() 的图象开口向上,对称轴为直线
的图象开口向上,对称轴为直线![]() .
.
(i)当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,则
上单调递增,则![]() ,
,![]() ,即
,即![]() ,
,
此时,函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,
,
由题意可得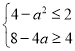 ,解得
,解得![]() ,此时,
,此时,![]() ;
;
(ii)当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,则
上单调递增,则![]() ,
,![]() ,即
,即![]() ,
,
此时,函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,
,
由题意可得![]() ,解得
,解得![]() 或
或![]() ,此时
,此时![]() ;
;
(iii)当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,则
上单调递减,则![]() ,
,![]() ,则函数
,则函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,
,
由题意可得![]() ,解得
,解得![]() ,此时,
,此时,![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知在![]() 中,
中,![]() ,且
,且![]() .
.
(1)求角![]() 的大小;
的大小;
(2)设数列![]() 满足
满足![]() ,前
,前![]() 项和为
项和为![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:
(1)由题意结合三角形内角和为![]() 可得
可得![]() .由余弦定理可得
.由余弦定理可得![]() ,,结合勾股定理可知
,,结合勾股定理可知![]() 为直角三角形,
为直角三角形,![]() ,
,![]() .
.
(2)结合(1)中的结论可得![]()
![]() .则
.则![]()
![]() ,
,![]() 据此可得关于实数k的方程
据此可得关于实数k的方程![]() ,解方程可得
,解方程可得![]() ,则
,则![]() 或
或![]() .
.
试题解析:
(1)由已知![]() ,又
,又![]() ,所以
,所以![]() .又由
.又由![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() 为直角三角形,
为直角三角形,![]() ,
,![]() .
.
(2)![]()
![]() .
.
所以![]()
![]()
![]() ,
,![]() 由
由![]() ,得
,得
![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() 或
或![]() .
.
【题型】解答题
【结束】
18
【题目】已知点![]() 是平行四边形
是平行四边形![]() 所在平面外一点,如果
所在平面外一点,如果![]() ,
,![]() ,
,![]() .(1)求证:
.(1)求证:![]() 是平面
是平面![]() 的法向量;
的法向量;
(2)求平行四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的点,
上的点,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得
的位置,使得![]() ,如图2.
,如图2.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过圆![]() :
:![]() 上的点
上的点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 满足
满足![]() .当
.当![]() 在
在![]() 上运动时,记点
上运动时,记点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与圆
两点,与圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家为了了解一款产品的质量,随机抽取200名男性使用者和100名女性使用者,对该款产品进行评分,绘制出如下频率分布直方图.

(1)利用组中值(数据分组后,一个小组的组中值是指这个小组的两个端点的数的平均数),估计100名女性使用者评分的平均值;
(2)根据评分的不同,运用分层抽样从这200名男性中抽取20名,在这20名中,从评分不低于80分的人中任意抽取3名,求这3名男性中恰有一名评分在区间![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的程序框图中,若输入![]() ,
,![]() ,则输出的
,则输出的![]() 值是( )
值是( )
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/3/21/1907086498037760/1907898837975040/STEM/25d20caaa911497ea3baaf4f7dee45a3.png]
A. 3 B. 7 C. 11 D. 33
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 是菱形,
是菱形,![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com