
【题目】已知函数![]() .
.
(1)若![]() 的零点为2,求
的零点为2,求![]() ;
;
(2)若![]() 在
在![]() 上单调递减,求
上单调递减,求![]() 的最小值;
的最小值;
(3)若对于任意的![]() 都有
都有![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ; (2)
; (2)![]() ; (3)
; (3)![]() .
.
【解析】
(1)由![]() 的零点为2,即
的零点为2,即![]() ,得到
,得到![]() ,即可求解实数
,即可求解实数![]() 的值;
的值;
(2)求得函数![]() 的定义域即函数的定义域为
的定义域即函数的定义域为![]() 且
且![]() ,设
,设![]() ,
,
根据复数函数的单调性,得到![]() ,即可求解;
,即可求解;
(3)由(2)中函数的定义域,利用复合数函数的单调性,要使得对于任意的![]() 都有
都有![]() ,得到
,得到![]() ,即可求解.
,即可求解.
(1)由题意,函数![]() ,
,
因为![]() 的零点为2,即
的零点为2,即![]() ,所以
,所以![]() ,
,
即![]() ,则
,则![]() ,即
,即![]() ,解得
,解得![]() .
.
(2)由![]() ,
,
可得函数![]() 满足
满足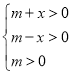 ,解得
,解得![]() 且
且![]() ,
,
即函数的定义域为![]() ,
,
又由函数![]() ,
,
设![]() ,
,
要使得函数![]() 在
在![]() 上单调递减,
上单调递减,
根据复合函数的单调性,可得函数![]() 在
在![]() 上单调递减,且
上单调递减,且![]() 在
在![]() 恒成立,
恒成立,
所以![]() ,解得
,解得![]() 或
或![]() ,
,
又因为![]() ,所以
,所以![]() ,即实数
,即实数![]() 的最小值为
的最小值为![]() .
.
(3)由(2)得![]() ,函数的定义域为
,函数的定义域为![]() 且
且![]()
根据复合函数的单调性,可得函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
要使得对于任意的![]() 都有
都有![]() ,
,
可得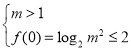 ,即
,即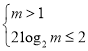 ,解得
,解得![]() ,
,
即实数![]() 的取值范围是
的取值范围是![]() .
.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)函数![]() 与函数
与函数![]() 的图像总有两个交点,设这两个交点的横坐标分别为
的图像总有两个交点,设这两个交点的横坐标分别为![]() ,
,![]() .
.
(ⅰ)求![]() 的取值范围;
的取值范围;
(ⅱ)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国城市空气污染指数范围及相应的空气质量类别见下表:
空气污染指数 | 空气质量 | 空气污染指数 | 空气质量 | |
0--50 | 优 | 201--250 | 中度污染 | |
51--100 | 良 | 251--300 | 中度重污染 | |
101--150 | 轻微污染 | >300 | 重污染 | |
151----200 | 轻度污染 |
我们把某天的空气污染指数在0-100时称作A类天,101--200时称作B类天,大于200时称作C类天.下图是某市2014年全年监测数据中随机抽取的18天数据作为样本,其茎叶图如下:(百位为茎,十.个位为叶)

(1)从这18天中任取3天,求至少含2个A类天的概率;
(2)从这18天中任取3天,记X是达到A类或B类天的天数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为提高员工的综合素质,聘请专业机构对员工进行专业技术培训,其中培训机构费用成本为12000元.公司每位员工的培训费用按以下方式与该机构结算:若公司参加培训的员工人数不超过30人时,每人的培训费用为850元;若公司参加培训的员工人数多于30人,则给予优惠:每多一人,培训费减少10元.已知该公司最多有60位员工可参加培训,设参加培训的员工人数为![]() 人,每位员工的培训费为
人,每位员工的培训费为![]() 元,培训机构的利润为
元,培训机构的利润为![]() 元.
元.
(1)写出![]() 与
与![]()
![]() 之间的函数关系式;
之间的函数关系式;
(2)当公司参加培训的员工为多少人时,培训机构可获得最大利润?并求最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com