
【题目】(选修4-5:不等式选讲)
设函数![]()
(1)若a=1,试求![]() 的解集;
的解集;
(2)若a>0,且关于x的不等式![]() 有解,求实数a的取值范围
有解,求实数a的取值范围
【答案】(1)![]() .(2)
.(2)![]()
【解析】试题分析:(1)由零点分段法分三段求不等式![]() 的解集.
的解集.
(2)关于![]() 的不等式
的不等式![]() 有解,则函数
有解,则函数![]() 的图象与直线
的图象与直线![]() 有两个交点,从而可求实数
有两个交点,从而可求实数![]() 的取值范围.
的取值范围.
试题解析:(1)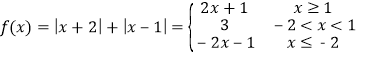
由![]() 得
得![]() ; 由
; 由![]() ,此不等式无解,由
,此不等式无解,由![]() 得
得![]() ,
,
故不等式![]() 的解集为
的解集为![]() .
.
(2)当![]() 时,
时,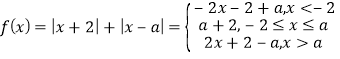
若关于![]() 的不等式
的不等式![]() 有解,则函数
有解,则函数![]() 的图象与直线
的图象与直线![]() 有两个交点,
有两个交点,
∴![]() ,解得
,解得![]() ,∴实数
,∴实数![]() 的取值范围是
的取值范围是![]() .
.
点晴:含绝对值不等式的解法有两个基本方法,一是运用零点分区间讨论,二是利用对值的几何意义求解.法一是运用分类讨论的思想,法二是运用数形结合思想,将绝对值不等式与函数以及不等式恒成立交汇、渗透,解题时强化函数、数形结合与转化化归思想方法的灵活应用,这是命题的新动向.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】空气质量主要受污染物排放量及大气扩散等因素的影响,某市环保监测站2014年10月连续10天(从左到右对应1号至10号)采集该市某地平均风速及空气中氧化物的日均浓度数据,制成散点图如图所示.
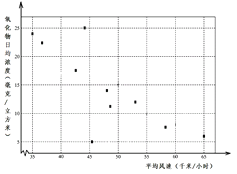
(Ⅰ)同学甲从这10天中随机抽取连续5天的一组数据,计算回归直线方程.试求连续5天的一组数据中恰好同时包含氧化物日均浓度最大与最小值的概率;
(Ⅱ)现有30名学生,每人任取5天数据,对应计算出30个不同的回归直线方程.已知30组数据中有包含氧化物日均浓度最值的有14组.现采用这30个回归方程对某一天平均风速下的氧化物日均浓度进行预测,若预测值与实测值差的绝对值小于2,则称之为“拟合效果好”,否则为“拟合效果不好”.根据以上信息完成下列2×2联表,并分析是否有95%以上的把握说拟合效果与选取数据是否包含氧化物日均浓度最值有关.
预测效果好 | 拟合效果不好 | 合计 | |
数据有包含最值 | 5 | ||
数据无包含最值 | 4 | ||
合计 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
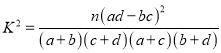 (其中
(其中![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的点,
上的点,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得
的位置,使得![]() ,如图2.
,如图2.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家为了了解一款产品的质量,随机抽取200名男性使用者和100名女性使用者,对该款产品进行评分,绘制出如下频率分布直方图.

(1)利用组中值(数据分组后,一个小组的组中值是指这个小组的两个端点的数的平均数),估计100名女性使用者评分的平均值;
(2)根据评分的不同,运用分层抽样从这200名男性中抽取20名,在这20名中,从评分不低于80分的人中任意抽取3名,求这3名男性中恰有一名评分在区间![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com