Question

18．设双曲线Γ的方程为x²-$\frac{{y}^{2}}{3}$=1，过其右焦点F且斜率不为零的直线l₁与双曲线交于A、B两点，直线l₂的方程为x=t，A、B在直线l₂上的射影分别为C、D．
（1）当l₁垂直于x轴，t=-2时，求四边形ABDC的面积；
（2）当t=0，l₁的斜率为正实数，A在第一象限，B在第四象限时，试比较$\frac{|AC|•|FB|}{|BD|•|FA|}$和1的大小，并说明理由；
（3）是否存在实数t∈（-1，1），使得对满足题意的任意直线l₁，直线AD和直线BC的交点总在x轴上，若存在，求出所有的t的值和此时直线AD与BC交点的位置；若不存在，说明理由．

Answer 1

分析 （1）由双曲线Γ的方程为x²-$\frac{{y}^{2}}{3}$=1，可得c=$\sqrt{1+3}$=2，可得右焦点F（2，0）．当l₁垂直于x轴，t=-2时，由双曲线的对称性可得：四边形ABDC为矩形．即可得出面积．
（2）作出右准线MN：x=$\frac{1}{2}$．e=$\frac{c}{a}$=2．分别作AC⊥MN，垂足为M；BD⊥MN，垂足为N．利用双曲线的第二定义可得：$\frac{|AC|}{|AF|}$=$\frac{|AM|+\frac{1}{2}}{|AF|}$，$\frac{|FB|}{|BD|}$=$\frac{1}{\frac{|BD|}{|FB|}}$=$\frac{1}{\frac{|BN|+\frac{1}{2}}{|FB|}}$．
（3）存在实数t∈（-1，1），t=$\frac{1}{2}$时，定点$（\frac{5}{4}，0）$．下面给出证明分析：设直线AB的方程为：y=k（x-2），A（x₁，k（x₁-2）），B（x₂，k（x₂-2））．则C（t，k（x₁-2）），D（t，k（x₂-2））．直线方程与双曲线方程联立化为：（3-k²）x²+4k²x-4k²-3=0，分别得出：直线AD与BC的方程，进而得出．

解答 解：（1）由双曲线Γ的方程为x²-$\frac{{y}^{2}}{3}$=1，可得c=$\sqrt{1+3}$=2，可得右焦点F（2，0）．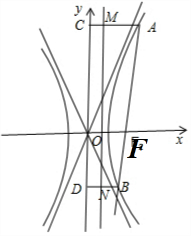
当l₁垂直于x轴，t=-2时，由双曲线的对称性可得：四边形ABDC为矩形．
代入双曲线可得：2²-$\frac{{y}^{2}}{3}$=1，焦点y=±3．
∴四边形ABDC的面积S=4×6=24．
（2）作出右准线MN：x=$\frac{1}{2}$．e=$\frac{c}{a}$=2．
分别作AC⊥MN，垂足为M；BD⊥MN，垂足为N．
则$\frac{|AC|}{|AF|}$=$\frac{|AM|+\frac{1}{2}}{|AF|}$=$\frac{1}{2}$+$\frac{1}{2|AF|}$．
$\frac{|FB|}{|BD|}$=$\frac{1}{\frac{|BD|}{|FB|}}$=$\frac{1}{\frac{|BN|+\frac{1}{2}}{|FB|}}$=$\frac{1}{\frac{1}{2}+\frac{1}{2|FB|}}$．
∵|AF|＞|FB|，∴$\frac{1}{|AF|}$＜$\frac{1}{|FB|}$．
∴$\frac{|AC|•|FB|}{|BD|•|FA|}$＜1．
（3）存在实数t∈（-1，1），t=$\frac{1}{2}$时，定点$（\frac{5}{4}，0）$．下面给出证明：
设直线AB的方程为：y=k（x-2），A（x₁，k（x₁-2）），B（x₂，k（x₂-2））．
则C（t，k（x₁-2）），D（t，k（x₂-2））．
 联立$\left\{\begin{array}{l}{y=k（x-2）}\\{{x}^{2}-\frac{{y}^{2}}{3}=1}\end{array}\right.$，化为：（3-k²）x²+4k²x-4k²-3=0，
可得x₁+x₂=$\frac{-4{k}^{2}}{3-{k}^{2}}$，x₁•x₂=$\frac{-4{k}^{2}-3}{3-{k}^{2}}$．
直线AD的方程为：y-k（x₁-2）=$\frac{k（{x}_{1}-{x}_{2}）}{{x}_{1}-t}$（x-x₁），令y=0，解得x=$\frac{2{x}_{1}-2t+t{x}_{1}-{x}_{1}{x}_{2}}{{x}_{1}-{x}_{2}}$．
直线BC的方程为：y-k（x₂-2）=$\frac{k（{x}_{1}-{x}_{2}）}{t-{x}_{2}}$（x-x₂），令y=0，解得x=$\frac{2t-2{x}_{2}-t{x}_{2}+{x}_{1}{x}_{2}}{{x}_{1}-{x}_{2}}$．
由$\frac{2{x}_{1}-2t+t{x}_{1}-{x}_{1}{x}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{2t-2{x}_{2}-t{x}_{2}+{x}_{1}{x}_{2}}{{x}_{1}-{x}_{2}}$，可得：（2+t）（x₁+x₂）-2x₁•x₂-4t=0．
∴（2+t）•$\frac{-4{k}^{2}}{3-{k}^{2}}$-2•$\frac{-4{k}^{2}-3}{3-{k}^{2}}$-4t=0．
化为：t=$\frac{1}{2}$，不妨取k=1，则2x²+4x-7=0，
解得x=$\frac{-2±3\sqrt{2}}{2}$．不妨取x₁=$\frac{-2+3\sqrt{2}}{2}$，x₂=$\frac{-2-3\sqrt{2}}{2}$．
定点的横坐标x=$\frac{2{x}_{1}-1+\frac{1}{2}{x}_{1}-{x}_{1}{x}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{\frac{5}{2}×\frac{-2+3\sqrt{2}}{2}-1-（-\frac{7}{2}）}{3\sqrt{2}}$=$\frac{5}{4}$．
∴定点坐标$（\frac{5}{4}，0）$．

点评 本题考查了双曲线的第二定义、直线与双曲线相交问题、一元二次方程的根与系数的关系、直线过定点问题，考查了推理能力与计算能力，属于难题．