
科目:高中数学 来源: 题型:
如图5, 为坐标原点,双曲线
为坐标原点,双曲线 和椭圆
和椭圆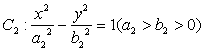 均过点
均过点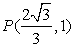 ,且以
,且以 的两个顶点和
的两个顶点和 的两个焦点为顶点的四边形是面积为2的正方形.
的两个焦点为顶点的四边形是面积为2的正方形.
求 的方程;
的方程;
是否存在直线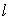 ,使得
,使得 与
与 交于
交于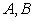 两点,与
两点,与 只有一个公共点,且
只有一个公共点,且 ?证明你的结论.
?证明你的结论.

查看答案和解析>>
科目:高中数学 来源: 题型:
已知向量 =
= ,
,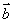 =(cos x,-1).
=(cos x,-1).
(1)当向量 ∥
∥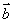 时,求cos2x-sin 2x的值;
时,求cos2x-sin 2x的值;
(2)设函数f(x)=2( +
+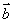 )·
)·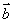 ,已知在△ABC中,内角A,B,C的对边分别为a,b,c,若a=
,已知在△ABC中,内角A,B,C的对边分别为a,b,c,若a= ,b=2,sin B=
,b=2,sin B=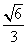 ,求f(x)+4cos(2A+
,求f(x)+4cos(2A+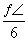 )(x∈[0,
)(x∈[0, ])的取值范围.
])的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
有3名男生,4名女生,在下列不同要求下,求不同的排列方法总数.
(1)全体排成一行,其中甲只能在中间或者两边位置;
(2)全体排成一行,男生不能排在一起;
(3)全体排成一行,其中甲、乙、丙三人从左至右的顺序不变;
(4)全体排成一行,甲、乙两人中间必须有3人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com