练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数的定义域为，其中， 为自然对数的底数.

    （1）设是函数的导函数，讨论的单调性；

    （2）若关于的方程在上有解，求实数的取值范围.

    【答案】（1）见解析；（2）

    【解析】试题分析：⑴先求出，然后求导，分类、、时三种情况讨论得出结果(2)构造，求导，分类讨论、、时零点情况

    解析：（1）∵，∴；

    由于

    ∴当时， ，此时在上单调递增；

    当时， ，此时在上单调递减；

    当时， ， ，此时在上单调递减，在上单调递增

    （2）依题意，即有零点，

    ∵； ， ，

    由（1）知，当时， 在上单调递增， ， ；

    ∴存在使得，且当时，故递减，当

    时，故递增；∴，无零点；

    当时， 在上单调递减， ， ，∴存在使得

    ，且当时，故递增，当时

    ，故递减；∴，无零点；

    当时， 在上单调递减，在上单调递增；

    ∴有零点 ，

    令，则，

    ∴，

    则，∴此时，综上：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）试判断1是的极大值点还是极小值点，并说明理由；

    （Ⅱ）设是函数的导函数，求证： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知， 分别为双曲线： 的左、右焦点，过的直线与双曲线的左右两支分别交于， 两点，若，则双曲线的离心率为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两人在相同条件下各射靶10次，每次射靶的成绩情况如图所示：

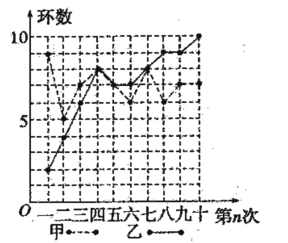
    （Ⅰ）请填写下表（写出计算过程）：

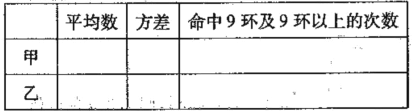
    （Ⅱ）从下列三个不同的角度对这次测试结果进行分析；

    ①从平均数和方差相结合看（分析谁的成绩更稳定）；

    ②从平均数和命中9环及9环以上的次数相结合看（分析谁的成绩好些）；

    ③从折线图上两人射击命中环数的走势看（分析谁更有潜力）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设椭圆C： ，定义椭圆C的“相关圆”方程为，若抛物线的焦点与椭圆C的一个焦点重合，且椭圆C短轴的一个端点和其两个焦点构成直角三角形。

    （I）求椭圆C的方程和“相关圆”E的方程；

    （II）过“相关圆”E上任意一点P作“相关圆”E的切线l与椭圆C交于A，B两点，O为坐标原点。

    （i）证明∠AOB为定值；

    （ii）连接PO并延长交“相关圆”E于点Q，求△ABQ面积的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的定义域为，且对任意的有. 当时，，.

    （1）求并证明的奇偶性；

    （2）判断的单调性并证明；

    （3）求；若对任意恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，是一个半圆柱与多面体构成的几何体，平面与半圆柱的下底面共面，且， 为弧上（不与重合）的动点.

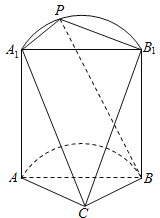
    （1）证明： 平面；

    （2）若四边形为正方形，且， ，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，从一个面积为的半圆形铁皮上截取两个高度均为的矩形，并将截得的两块矩形铁皮分别以，为母线卷成两个高均为的圆柱（无底面，连接部分材料损失忽略不计）．记这两个圆柱的体积之和为．

    （1）将表示成的函数关系式，并写出的取值范围；

    （2）求两个圆柱体积之和的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P—ABCD中，底面ABCD为矩形，DP⊥平面PBC，E，F分别为PA与BC的中点．

    （1）求证：BC⊥平面PDC；

    （2）求证：EF//平面PDC．

    查看答案和解析>>

    同步练习册答案