
【题目】如图,在三棱柱![]() 中,四边形
中,四边形![]() ,
,![]() 均为正方形,且
均为正方形,且![]() ,M为
,M为![]() 的中点,N为
的中点,N为![]() 的中点.
的中点.
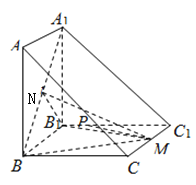
(1)求证:![]() 平面ABC;
平面ABC;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)设P是棱![]() 上一点,若直线PM与平面
上一点,若直线PM与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值
的值
【答案】(1)证明过程见详解;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先取![]() 中点为
中点为![]() ,连接
,连接![]() ,
,![]() ,根据面面平行的判定定理,得到平面
,根据面面平行的判定定理,得到平面![]() 平面
平面![]() ,进而可得
,进而可得![]() 平面ABC;
平面ABC;
(2)先由题意,得到![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,设
轴建立空间直角坐标系,设![]() 边长为
边长为![]() ,分别求出平面
,分别求出平面![]() 和平面
和平面![]() 的一个法向量,根据向量夹角公式,求解,即可得出结果;
的一个法向量,根据向量夹角公式,求解,即可得出结果;
(3)先设![]() ,得到
,得到![]() ,根据空间向量的夹角公式,列出等式求解,即可得出结果.
,根据空间向量的夹角公式,列出等式求解,即可得出结果.
(1)取![]() 中点为
中点为![]() ,连接
,连接![]() ,
,![]() ,
,
因为![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,
所以![]() ,
,![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以![]() 平面ABC;
平面ABC;
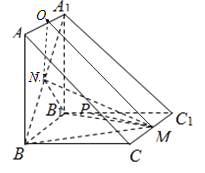
(2)因为四边形![]() ,
,![]() 均为正方形,所以
均为正方形,所以![]() ,
,![]() ,
,![]() 两两垂直,
两两垂直,
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系,设
轴建立如图所示的空间直角坐标系,设![]() 边长为
边长为![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
因此![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则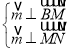 ,所以
,所以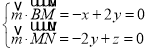 ,令
,令![]() ,则
,则![]() ,
,
因此![]() ;
;
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则 ,所以
,所以 ,令
,令![]() ,则
,则![]() ,
,
因此![]() ,
,
设二面角![]() 的大小为
的大小为![]() ,
,
则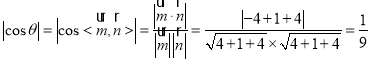 ,
,
所以![]() ;
;
(3)因为![]() 是棱
是棱![]() 上一点,设
上一点,设![]() ,则
,则![]() ,
,
所以![]() ,
,
由(2)知,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
又直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,记直线
,记直线![]() 与平面
与平面![]() 所成角为
所成角为![]()
则有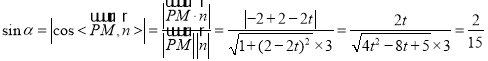 ,
,
整理得![]() ,解得
,解得![]() 或
或![]() (舍)
(舍)
所以![]() .
.



 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】2019冠状病毒病(CoronaVirus Disease2019(COVID-19))是由新型冠状病毒(2019-nCoV)引发的疾病,目前全球感染者以百万计,我国在党中央、国务院、中央军委的坚强领导下,已经率先控制住疫情,但目前疫情防控形势依然严峻,湖北省中小学依然延期开学,所有学生按照停课不停学的要求,居家学习.小李同学在居家学习期间,从网上购买了一套高考数学冲刺模拟试卷,快递员计划在下午4:00~5:00之间送货到小区门口的快递柜中,小李同学父亲参加防疫志愿服务,按规定,他换班回家的时间在下午4:30~5:00,则小李父亲收到试卷无需等待的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某景点共有999级台阶,寓意长长久久.游客甲上台阶时,可以一步走一个台阶,也可以一步走两个台阶,无其它可能.若甲每步上一个台阶的概率为![]() ,每步上两个台阶的概率也为
,每步上两个台阶的概率也为![]() .为了简便描述问题,我们约定,甲从0级台阶开始向上走,一步走一个台阶记1分,一步走两个台阶记2分,记甲登上第
.为了简便描述问题,我们约定,甲从0级台阶开始向上走,一步走一个台阶记1分,一步走两个台阶记2分,记甲登上第![]() 个台阶的概率为
个台阶的概率为![]() ,其中
,其中![]() ,且
,且![]() .
.
(1)甲走3步时所得分数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)证明:当![]() ,且
,且![]() 时,数列
时,数列![]() 是等比数列,并求甲登上第100级台阶的概率
是等比数列,并求甲登上第100级台阶的概率![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,椭圆
,椭圆![]() 上一点
上一点![]() 与两焦点构成的三角形的周长为6,离心率为
与两焦点构成的三角形的周长为6,离心率为![]() ,
,
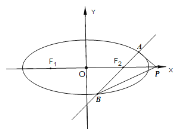
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,问在
两点,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?证明你的结论.
为定值?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现给出三个条件:①函数![]() 的图象关于直线
的图象关于直线![]() 对称;②函数
对称;②函数![]() 的图象关于点
的图象关于点![]() 对称;③函数
对称;③函数![]() 的图象上相邻两个最高点的距离为
的图象上相邻两个最高点的距离为![]() .从中选出两个条件补充在下面的问题中,并以此为依据求解问题.
.从中选出两个条件补充在下面的问题中,并以此为依据求解问题.
已知函数![]() (
(![]() ,
,![]() ),_____,_____.求函数
),_____,_____.求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B是椭圆C:![]() )的左右顶点,P点为椭圆C上一点,点P关于x轴的对称点为H,且
)的左右顶点,P点为椭圆C上一点,点P关于x轴的对称点为H,且![]()
(1)若椭圆C经过了圆![]() 的圆心,求椭圆C的标准方程;
的圆心,求椭圆C的标准方程;
(2)在(1)的条件下,抛物线D:![]() 的焦点F与点
的焦点F与点![]() 关于y轴上某点对称,且抛物线D与椭圆C在第四象限交于点Q,过点Q作直线与抛物线D有唯一公共点,求该直线与两坐标轴围成的三角形面积.
关于y轴上某点对称,且抛物线D与椭圆C在第四象限交于点Q,过点Q作直线与抛物线D有唯一公共点,求该直线与两坐标轴围成的三角形面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校运动会男生组田径综合赛以选手三项运动的综合积分高低决定排名.具体积分规则如表1所示,某代表队四名男生的模拟成绩如表2.
表1 田径综合赛项目及积分规则
项目 | 积分规则 |
| 以 |
跳高 | 以 |
掷实心球 | 以 |
表2 某队模拟成绩明细
姓名 | 100米跑(秒) | 跳高(米) | 掷实心球(米) |
甲 |
|
|
|
乙 |
|
|
|
丙 |
|
|
|
丁 |
|
|
|
根据模拟成绩,该代表队应选派参赛的队员是:( )
A.甲B.乙C.丙D.丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某湿地公园的鸟瞰图是一个直角梯形,其中:![]() ,
,![]() ,
,![]() ,
,![]() 长1千米,
长1千米,![]() 长
长![]() 千米,公园内有一个形状是扇形的天然湖泊
千米,公园内有一个形状是扇形的天然湖泊![]() ,扇形
,扇形![]() 以
以![]() 长为半径,弧
长为半径,弧![]() 为湖岸,其余部分为滩地,B,D点是公园的进出口.公园管理方计划在进出口之间建造一条观光步行道:线段
为湖岸,其余部分为滩地,B,D点是公园的进出口.公园管理方计划在进出口之间建造一条观光步行道:线段![]() 线段
线段![]() 弧
弧![]() ,其中Q在线段
,其中Q在线段![]() 上(异于线段端点),
上(异于线段端点),![]() 与弧
与弧![]() 相切于P点(异于弧端点]根据市场行情
相切于P点(异于弧端点]根据市场行情![]() ,
,![]() 段的建造费用是每千米10万元,湖岸段弧
段的建造费用是每千米10万元,湖岸段弧![]() 的建造费用是每千米
的建造费用是每千米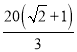 万元(步行道的宽度不计),设
万元(步行道的宽度不计),设![]() 为
为![]() 弧度观光步行道的建造费用为
弧度观光步行道的建造费用为![]() 万元.
万元.
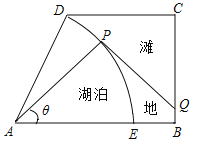
(1)求步行道的建造费用![]() 关于
关于![]() 的函数关系式,并求其走义域;
的函数关系式,并求其走义域;
(2)当![]() 为何值时,步行道的建造费用最低?
为何值时,步行道的建造费用最低?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com