
已知函数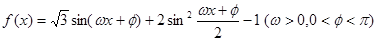 为奇函数,且相邻两对称轴间的距离为
为奇函数,且相邻两对称轴间的距离为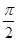 .
.
(1)当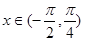 时,求
时,求 的单调递减区间;
的单调递减区间;
(2)将函数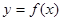 的图象沿
的图象沿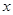 轴方向向右平移
轴方向向右平移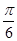 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的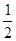 (纵坐标不变),得到函数
(纵坐标不变),得到函数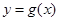 的图象.当
的图象.当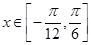 时,求函数
时,求函数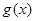 的值域.
的值域.
(1)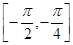 ;(2)
;(2)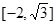
解析试题分析:(1)先用余弦二倍角公式将其降幂,再用两角和差公式的逆用即化一公式将其化简为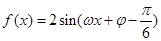 ,两相邻对称轴间的距离为半个周期,从而可得
,两相邻对称轴间的距离为半个周期,从而可得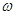 的值,由函数为奇函数可求
的值,由函数为奇函数可求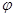 的值。根据
的值。根据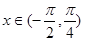 求整体角的范围。再此范围内将整体角代入正弦的单调减区,解得
求整体角的范围。再此范围内将整体角代入正弦的单调减区,解得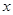 的范围,即为所求。(2)先将
的范围,即为所求。(2)先将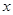 用
用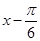 替换,再将
替换,再将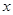 用
用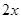 替换即可得函数
替换即可得函数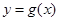 。根据
。根据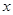 的范围得整体角的范围,结合函数图像求函数的值域。
的范围得整体角的范围,结合函数图像求函数的值域。
(1)由题知 ,
,
∵相邻两对称轴的距离为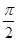 ,∴
,∴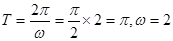 , 3分
, 3分
又∵ 为奇函数,∴
为奇函数,∴ ,
,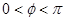 , ∴
, ∴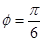 , 即
, 即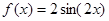 , 5分
, 5分
要使 单调递减, 需
单调递减, 需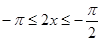 ,
,  ,
,
∴ 的单调减区间为
的单调减区间为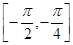 . 7分
. 7分
(2) 由题知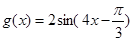 , 9分
, 9分
∵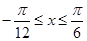 , ∴
, ∴ ,
, 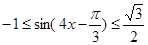 ,
,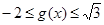 ,
,
∴函数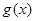 的值域为
的值域为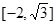 12分
12分
考点:1三角函数的周期性奇偶性;2三角函数的单调性;3三角函数伸缩平移变换。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
函数f(x)=6cos2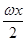 +
+ sin ωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
sin ωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.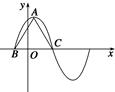
(1)求ω的值及函数f(x)的值域;
(2)若f(x0)=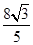 ,且x0∈
,且x0∈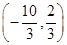 ,求f(x0+1)的值.
,求f(x0+1)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com