练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．在△ABC中，D是BC的中点，|$\overrightarrow{AD}$|=3，点P在AD上，且满足$\overrightarrow{AP}$=$\frac{1}{2}$$\overrightarrow{PD}$，则$\overrightarrow{PA}$•（$\overrightarrow{PB}$+$\overrightarrow{PC}$）=（　　）
    A．4B．2C．-2D．-4

    分析 由题意可得|$\overrightarrow{PA}$|=$\frac{1}{3}$|$\overrightarrow{AD}$|=1，|$\overrightarrow{PD}$|=2，再由中点的向量表示，可得$\overrightarrow{PA}$•（$\overrightarrow{PB}$+$\overrightarrow{PC}$）=2$\overrightarrow{PA}$•$\overrightarrow{PD}$，运用向量的数量积的定义，计算即可得到所求值．

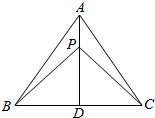    解答 解：由|$\overrightarrow{AD}$|=3，点P在AD上，且满足$\overrightarrow{AP}$=$\frac{1}{2}$$\overrightarrow{PD}$，
    可得|$\overrightarrow{PA}$|=$\frac{1}{3}$|$\overrightarrow{AD}$|=1，|$\overrightarrow{PD}$|=2，
    由D是BC的中点，可得2$\overrightarrow{PD}$=$\overrightarrow{PB}$+$\overrightarrow{PC}$，
    即有$\overrightarrow{PA}$•（$\overrightarrow{PB}$+$\overrightarrow{PC}$）=2$\overrightarrow{PA}$•$\overrightarrow{PD}$
    =-2|$\overrightarrow{PA}$|•|$\overrightarrow{PD}$|=-2×1×2=-4．
    故选D．

    点评 本题考查向量的数量积的定义，考查中点的向量表示形式，考查运算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    18．在边长为1的正方形ABCD中任取一点P，则△ABP的面积大于$\frac{1}{4}$的概率是$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．如图，在四边形ABCD中，$\overrightarrow{AB}$=$\overrightarrow{DC}$，N、M分是AD、BC上的点，且$\overrightarrow{CN}$=$\overrightarrow{MA}$，求证：$\overrightarrow{DN}$=$\overrightarrow{MB}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．若不等式x2-2mx+m2-1＜0成立的必要不充分条件是$\frac{1}{3}$＜x＜$\frac{7}{2}$，则实数m的取值范围是（　　）
    A．（-∞，$\frac{4}{3}$]∪[$\frac{5}{2}$，+∞）B．（-∞，$\frac{4}{3}$]∪（$\frac{5}{2}$，+∞）C．[$\frac{4}{3}$，$\frac{5}{2}$]D．[$\frac{4}{3}$，$\frac{5}{2}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．设函数f（x）=$\left\{\begin{array}{l}{{x}^{3}，}&{x≥a}\\{-{x}^{2}，}&{x＜a}\end{array}\right.$，a∈R，若存在实数b，使函数g（x）=f（x）-b有两个零点，则实数a的取值范围为（-∞，-1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知函数f（x）=|x2+3x|，x∈R，若方程f（x）-a|x-1|=0恰有4个互异的实数根，则实数a的取值范围为（0，1）∪（9，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知数列{an}为等差数列，且a5+a7+a9+a11+a13=80，则a14+a16-a21=（　　）
    A．12B．15C．16D．18

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．求下列函数定义域．
    （1）y=tan$\frac{x}{2}$      
    （2）y=$\frac{1}{1-tanx}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．在三棱锥C-ABD中，△ABD与△CBD是全等的等腰直角三角形，O为斜边BD的中点，AB=4，二面角A-BD-C的大小为$\frac{π}{6}$并给出下面结论：
    （1）AC⊥BD；  （2）AD⊥CO；  （3）△AOC为正三角形； （4）cos∠ADC=$\frac{3}{4}$；
    （5）四面体ABCD的外接球表面积为32π，
    其中真命题个数是（1）（5）．

    查看答案和解析>>

    同步练习册答案