练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．如图，在四边形ABCD中，$\overrightarrow{AB}$=$\overrightarrow{DC}$，N、M分是AD、BC上的点，且$\overrightarrow{CN}$=$\overrightarrow{MA}$，求证：$\overrightarrow{DN}$=$\overrightarrow{MB}$．

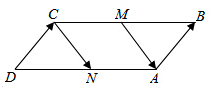
    分析 利用向量相等与向量的加法即可得出．

    解答 证明：∵$\overrightarrow{AB}$=$\overrightarrow{DC}$，N、M分是AD、BC上的点，且$\overrightarrow{CN}$=$\overrightarrow{MA}$，
    ∴$\overrightarrow{DC}$+$\overrightarrow{CN}$=$\overrightarrow{MA}$+$\overrightarrow{AB}$
    ∵$\overrightarrow{DN}$=$\overrightarrow{DC}$+$\overrightarrow{CN}$，$\overrightarrow{MB}$=$\overrightarrow{MA}$+$\overrightarrow{AB}$
    ∴$\overrightarrow{DN}$=$\overrightarrow{MB}$．

    点评 本题考查了向量相等与向量的加法，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    9．《中华人民共和国个人所得税法》规定，公民全月工资、薪金所得不超过3500元的部分不必纳税，超过3500元的部分为全月应纳税所得额．此项税款按下表分段累计计算：
    全月应纳税所得额税率（%）
    不超过1500元的部分3
    超过1500元至4500元的部分10
    超过4500元至9000元的部分20
    （1）设某人月工资、薪金所得为x元，求应纳税款Y的函数表达式？
    （2）某人一月份应交纳此项税款为303元，那么他当月的工资，薪金所得是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知X～N（μ，σ2）时，P（μ-σ＜X≤μ+σ）=0.6826，P（μ-2σ＜X≤μ+2σ）=0.9544，P（μ-3σ＜X≤μ+3σ）=0.9974，则$\int_3^4{\frac{1}{{\sqrt{2π}}}}{e^{-\frac{{{{（{x-1}）}^2}}}{2}}}$dx=（　　）
    A．0.043B．0.0215C．0.3413D．0.4772

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．下列四个函数中，在（0，+∞）上是增函数的是（　　）
    A．f（x）=3-xB．f（x）=x2-3xC．f（x）=x-1D．$f（x）={x^{\frac{1}{2}}}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．某小区设计一屋顶阁楼的截面图为等腰三角形，顶角为120°，腰长为4m，预备要开一矩形窗户，窗宽为x（m），试求：
    （1）窗户的采光面积y（m2）与窗宽x（m）之间的函数关系式及x的取值范围；
    （2）当窗户的长、宽分别为多少时，窗户的采光面积最大？并求出最大采光面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．若2kπ+π＜θ＜2kπ+$\frac{5π}{4}$（k∈Z），则sinθ，cosθ，tanθ的大小关系是cosθ＜sinθ＜tanθ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．设函数f（x）=ex（ax+b）．若曲线在点P（0，f（0））处的切线方程为y=4x+2．
    （Ⅰ）求a、b的值；
    （Ⅱ）求f（x）=ex（ax+b）的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．在△ABC中，D是BC的中点，|$\overrightarrow{AD}$|=3，点P在AD上，且满足$\overrightarrow{AP}$=$\frac{1}{2}$$\overrightarrow{PD}$，则$\overrightarrow{PA}$•（$\overrightarrow{PB}$+$\overrightarrow{PC}$）=（　　）
    A．4B．2C．-2D．-4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知定义在R上的一次函数f（x）满足f[f（x）-2x]=3，则f（x）的解析式为f（x）=2x+1．

    查看答案和解析>>

    同步练习册答案