
 已知海岛B在海岛A的北偏东45°方向上,A、B相距10海里,小船甲从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船乙从海岛A出发沿北偏15°方向也以2海里/小时的速度移动
已知海岛B在海岛A的北偏东45°方向上,A、B相距10海里,小船甲从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船乙从海岛A出发沿北偏15°方向也以2海里/小时的速度移动分析 (Ⅰ)利用余弦定理求|EF|的长度即可.
(Ⅱ)设经过t(0<t<5)小时小船甲处于小船乙的正东方向.利用正弦定理建立条件关系进行求解即可.
解答 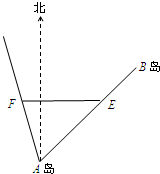 解:(Ⅰ)经过1小时后,甲船到达E点,乙船到达F点,
解:(Ⅰ)经过1小时后,甲船到达E点,乙船到达F点,
|AE|=10-2=8,|AF|=2,∠EAF=60°,┅┅┅┅┅┅┅┅┅┅┅┅┅2分
∴|EF|2=|AE|2+|AF|2-2|AE||AF|cos60°=64+4-2×$8×2×\frac{1}{2}$=52,
∴|EF|=2$\sqrt{13}$.┅┅┅┅┅┅┅┅┅┅┅┅┅┅5分
(Ⅱ)设经过t(0<t<5)小时小船甲处于小船乙的正东方向.
则甲船与A距离为|AE|=10-2t海里,乙船与A距离为|AF|=2t海里,∠EAF=60°,∠EFA=45°,┅┅┅6分
则由正弦定理得$\frac{|AE|}{sin45°}$=$\frac{|AF|}{sin75°}$,
即$\frac{2t}{sin45°}=\frac{10-2t}{sin75°}$,┅┅┅┅┅┅┅┅┅┅┅┅┅┅9分
则t=$\frac{10sin45°}{2sin75°+2sin45°}$=$\frac{10}{3+\sqrt{3}}$<5.┅┅┅┅┅┅┅┅11分
答:经过$\frac{10}{3+\sqrt{3}}$小时小船甲处于小船乙的正东方向.┅┅┅┅┅┅┅┅┅12分.
点评 本题主要考查解三角形的应用,根据正弦定理和余弦定理建立方程关系是解决本题的关键.


科目:高中数学 来源: 题型:解答题
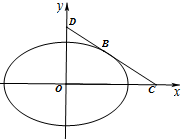 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),离心率e=$\frac{{\sqrt{2}}}{2}$,且过$(\frac{{\sqrt{6}}}{2},\frac{1}{2})$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),离心率e=$\frac{{\sqrt{2}}}{2}$,且过$(\frac{{\sqrt{6}}}{2},\frac{1}{2})$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-2y=0 | B. | x+2y=4 | C. | 2x+3y=14 | D. | x+2y=8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36$\sqrt{3}$+36 | B. | 6$\sqrt{3}$+6 | C. | 3$\sqrt{6}-3\sqrt{2}$ | D. | 18$\sqrt{6}-18\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥n,n∥α,则m⊥α | B. | 若m∥β,β⊥α则m⊥α | ||
| C. | 若m∥n,n⊥α则m⊥α | D. | 若m⊥n,n⊥β,β⊥α,则m⊥α |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com