
已知定义域为 的函数
的函数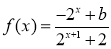 是奇函数。
是奇函数。
(1)求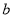 的值;
的值;
(2)判断函数 的单调性;
的单调性;
(3)若对任意的 ,不等式
,不等式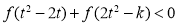 恒成立,求
恒成立,求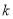 的取值范围.
的取值范围.
(1)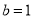 ;(2)
;(2)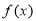 在
在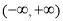 上为减函数;(3)
上为减函数;(3)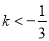 .
.
【解析】
试题分析:(1)因为函数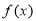 定义在
定义在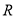 上的奇函数,所以对任意
上的奇函数,所以对任意 ,
, ,
,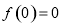 ;
;
(2)根据(1)的到的解析式,函数的单调性同过函数单调性的定义可判断,首先任取 ,然后作差比较
,然后作差比较 与
与 的大小,得到
的大小,得到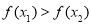 ,进而得
,进而得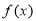 在
在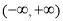 上为减函数;(3)显然通过代入解不等式计算难度很大,可以通过奇偶性和单调性解不等式,首先原不等式同解
上为减函数;(3)显然通过代入解不等式计算难度很大,可以通过奇偶性和单调性解不等式,首先原不等式同解
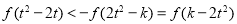 ,由(2)知
,由(2)知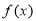 在
在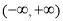 上为减函数,所以原不等式只需通过解
上为减函数,所以原不等式只需通过解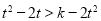 即:
即: 看成关于
看成关于 的二次函数,且
的二次函数,且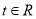 ,进而只需
,进而只需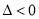 ,求得
,求得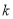 的取值范围.
的取值范围.
试题解析:(1)因为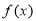 是奇函数,所以
是奇函数,所以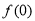 =0, (2分)
=0, (2分)
即 (4分)
(4分)
(2)由(1)知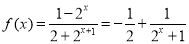 , (5分)
, (5分)
设 则
则 (6分)
(6分)
因为函数y=2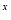 在R上是增函数且
在R上是增函数且 ∴
∴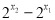 >0
>0
又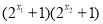 >0
>0
∴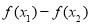 >0即
>0即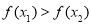 (8分)
(8分)
∴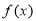 在
在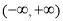 上为减函数. (9分)
上为减函数. (9分)
(3)因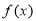 是奇函数,
是奇函数,
从而不等式: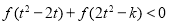
等价于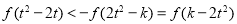 , (11分)
, (11分)
因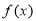 为减函数,由上式推得:
为减函数,由上式推得: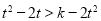 . (12分)
. (12分)
即对一切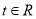 有:
有: , (13分)
, (13分)
从而判别式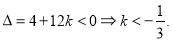 (14分)
(14分)
考点:1.函数的奇偶性;2.函数的单调性;3.解不等式.


科目:高中数学 来源:2014-2015学年江西省高二上学期期中考试文科数学试卷(解析版) 题型:选择题
已知A(-2,0),B(0,2),点C是圆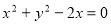 上任一点,则△ABC面积的最小值为
上任一点,则△ABC面积的最小值为
( )
A. B.
B. C.
C.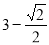 D.
D.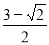
查看答案和解析>>
科目:高中数学 来源:2014-2015学年吉林省高二上学期期末考试理科数学试卷(解析版) 题型:选择题
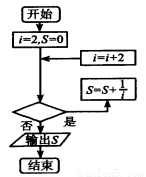
如图给出的是计算 的值的程序框图,其中判断框内应填入的是( ).
的值的程序框图,其中判断框内应填入的是( ).
A.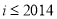 B.
B. C.
C.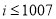 D.
D.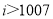
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省襄阳市等高二12月联考理科数学试卷(解析版) 题型:选择题
将参加夏令营的600名学生编号为:001,002, ,600.采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为004,这600名学生分住在三个营区.从001到300在第Ⅰ营区,从301到495在第Ⅱ营区,从496到600在第Ⅲ营区.三个营区被抽中的人数依次为( )
A.24,17,9 B.25,16,9 C.25,17,8 D.26,16,8
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高一上学期期末考试数学试卷(解析版) 题型:选择题
已知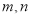 是两条不同直线,
是两条不同直线,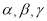 是三个不同平面,下列命题中正确的是( )
是三个不同平面,下列命题中正确的是( )
A.
B.
C.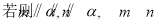
D.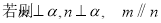
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com